一个骰子可以模拟出概率为1/7的结果吗?
- 1 个点赞 👍被审核的答案
连续投掷7次骰子,当这7次骰子中有且仅有一个1点的时候,投掷有效,其中1点是第几次投出来的,本次的投掷结果就算几点。
如若7次连续投掷结果中1点出现的次数不是1次,则投掷作废。重新开始投掷,直到连续7次投掷结果中有且仅有一个1点为止。
虽然可能需要投掷很多次才能投出有效投掷,但1点在第1-7次投掷中出现的概率确实都是1/7。
编辑于 2023-11-16 19:15・IP 属地上海查看全文>>
一只小牛马 - 3 个点赞 👍
丢两次。
如果丢到66就重新丢两次。
最终结果为豹子(11,22,33,44,55)的概率。
查看全文>>
成一一 - 2 个点赞 👍
前面的答案还是太复杂,我来最简单模型——投两次。
第一次摇骰子,单数记为A,双数记为B。
第二次摇骰子,如实记录点数。
两次结果(A/B+点数):
A1=1
A2=2
A3=3
A4=4
A5=5
A6=6
B1=7
B2=重新摇
B3=重新摇
B4=重新摇
B5=重新摇
B6=重新摇
可以轻松获得1/7的概率,也同样适用于1/8、1/9、1/10、1/11...等等。查看全文>>
Todd - 1 个点赞 👍
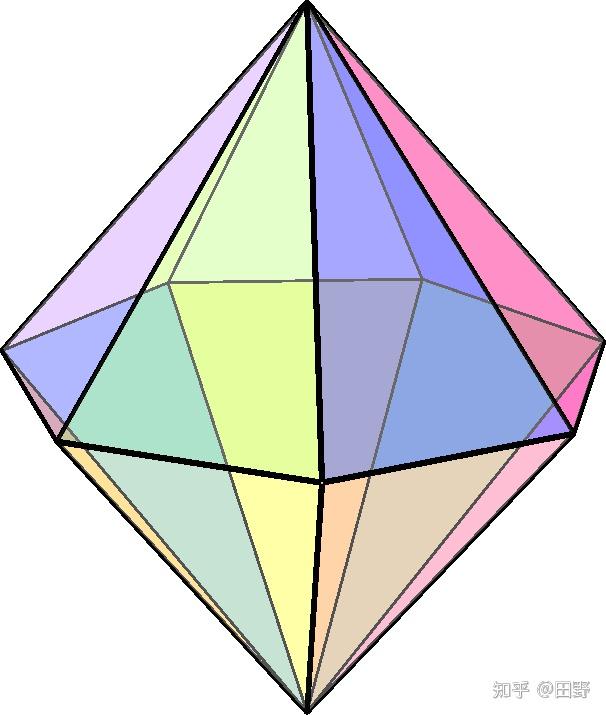
答案有七棱锥的 还有扔好多次的
我就说 正七面体存不存在我不清楚
不是有正14面体吗?
一扔解决
不好意思,半夜醒了写的。
我脑子里想的那个东西不叫正14面体。
就是两个正七边形为底的七角锥锥,底面对一起的一个双七角锥。
查看全文>>
田野 - 0 个点赞 👍
看了很多回答下的质疑,其实明白如何解答,至少要了解等比级数求和的公式。
对于首项为a,公比为q的等比数列。
- Sn = a(1-q^n)/(1-q) (q≠1)
- Sn = na (q=1)
当|q|<1时,n→∞,等比级数的和收敛于 S∞ = a/(1-q)。
基于这个认知,我们了解到连续投掷两个骰子会有 36 种情况。
我们去除其中一种情况得到 35,可以被 7 整除,则可以把这 35 种情况分成 7 类,每一类 5 种。
然后就是一个首项 5/36,公比为 1/36 的概率累计。
S∞ = a/(1-q) = 5/36(1 - 1/36) = 5/35 = 1/7。
查看全文>>
胖总 - 0 个点赞 👍
连着投掷七次, 点数相加。
然后当天的日期加上点数的天数, 结果指向的那一天是 星期几?
查看全文>>
正方行 - 493 个点赞 👍
查看全文>>
流浪的骆驼 - 466 个点赞 👍
连续投两次
- 如果第一次不是 6, 第二次是几就是几
- 如果第一次是 6, 第二次不是 6, 那它代表 7
- 如果第一第二次都是 6, 无效, 重新投两次
分析:
- 一: 11,21,31,41,51
- 二: 12,22,32,42,52
- 三: 13,23,33,43,53
- 四: 14,24,34,44,54
- 五: 15,25,35,45,55
- 六: 16,26,36,46,56
- 七: 61,62,63,64,65
- 无效: 66
36 种可能性取 35 种, 每个数字 5 个组合
发布于 2023-11-14 14:09・IP 属地上海查看全文>>
酱紫君 - 250 个点赞 👍
因为一个骰子可以掷多次,所以可以模拟出任何古典概型。我们可以将2次掷骰子设为一组试验,每组试验有6²=36种情况。这样,我们只要指定其中7种情况,然后重复多组试验,直到这7种情况中的1种出现为止。每种情况发生的概率是1/7。
发布于 2023-11-12 15:42・IP 属地黑龙江真诚赞赏,手留余香还没有人赞赏,快来当第一个赞赏的人吧!查看全文>>
33HCY - 158 个点赞 👍
最近程序员面试题涌进知乎,这是简单题。
第一问:怎么扔。立刻答:六面骰子扔两次,规定一种情况重扔,其余35种情况分成7组。
第二问:上述算法平均要扔几次?答:肯定是2次多一点,x = 2 + x * 1/36。
第三问:如果需要反复生成,而且假设扔骰子代价高昂,希望扔次数尽可能少,应该怎么做,理论最少几次?答:理论最少log_6(7)次,1次多一点,信息极限。一种实现方法是批量生成,比如一批扔12次骰子,可以生成11个结果,当然也可能需要再重扔12次。12和11是手动选的数字,也不一定就是最好。为了降低抖动,可能要加个队列。
更新:上述算法的输出是7个等概率的随机数,而非1/7概率的结果。
编辑于 2023-11-18 14:26・IP 属地北京查看全文>>
刘景詹 - 65 个点赞 👍
随机数转换的基本思路就是合并。
我们可以考虑一个比较简单的情况,如果我们用一个骰子去模拟概率为 \displaystyle \frac 1 5 ,我们应该怎么做呢?
很简单,我们可以直接选数字1-5为有效结果,如果投出6的话就再投,知道1-5出现为止。那么,我们投一次骰子,出现1的概率即为
\begin{aligned} P_{(1)} &= \displaystyle\frac 1 6 + \frac {1} 6 \cdot\frac 1 6 + (\frac 1 6)^2\cdot\frac 1 6+(\frac 1 6)^3\cdot\frac 1 6 + (\frac 1 6)^4\cdot\frac 1 6\cdots \\ &= \frac{1}{6}(1+\displaystyle \frac 16 +(\displaystyle \frac 16)^2 +(\displaystyle \frac 16)^3+ (\displaystyle \frac 16)^4\cdots) \\ &= \displaystyle\frac{\frac 16}{1-\frac 1 6} \\ & =\frac 15 \end{aligned}
很显然,当已有基本事件的个数较大时,上述构造是显然的。
那么,实际上我们只需要用六面骰子构造出超过7以上的等概率的基本事件,再用上述合并的方式并能正常构造出来了。
以本题为例,我们可以将骰子先后投两次,从而获得一个有序数对。这一数对涵盖了从 (1,1)\rightarrow(6,6) 三十六个基本事件。
\begin{bmatrix}(1,1)&(1,2)&(1,3)&(1,4)&(1,5)&(1,6)\\ (2,1)&(2,2)&(2,3)&(2,4)&(2,5)&(2,6)\\ (3,1)&(3,2)&(3,3)&(3,4)&(3,5)&(3,6)\\ (4,1)&(4,2)&(4,3)&(4,4)&(4,5)&(4,6)\\ (5,1)&(5,2)&(5,3)&(5,4)&(5,5)&(5,6)\\ (6,1)&(6,2)&(6,3)&(6,4)&(6,5)&\color{red}{(6,6)}\\\end{bmatrix}
当我们弃去其中一个事件,如 (6,6) 时,现有的35个基本事件就可以很好地构造出 \displaystyle \frac 1 7
编辑于 2023-11-13 19:54・IP 属地北京真诚赞赏,手留余香还没有人赞赏,快来当第一个赞赏的人吧!查看全文>>
阿克学长 - 26 个点赞 👍
可以
看上去6和7互质,所以不论摇几次骰子结果的数量都不能被7整除,但实际操作我们可以人为排除特定的结果改变结果的数量
例如,摇一次骰子,规定摇出6就重摇就能模拟出1/5的结果
同样的道理,依次摇两次骰子,有36个不同的结果,那么我们可以规定摇出66就重新摇,把其他35种结果分成7份,每一份出现的概率就是1/7了
发布于 2023-11-13 10:38・IP 属地湖南查看全文>>
愤怒的欢乐豆 - 17 个点赞 👍
把骰子削成一个七棱锥,投这个七棱锥,一直侧面着地为止。每个侧面的概率是1/7。
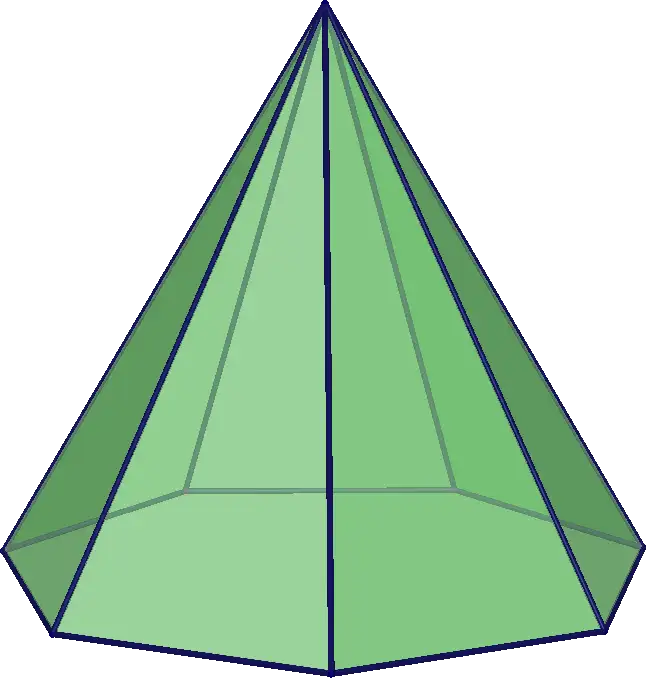
也可以把骰子削成一个六棱锥,调整削的角度使得6个侧面和底面的概率是1/7,这样投一次即可。由于计算过程太过复杂,留作习题(狗头)。
编辑于 2023-11-13 20:01・IP 属地北京查看全文>>
量化调酒师 - 6 个点赞 👍
查看全文>>
知乎用户C酱 - 2 个点赞 👍
查看全文>>
杨个毛 - 2 个点赞 👍
查看全文>>
林凌 - 1 个点赞 👍
焚香沐浴,虔诚地投下一枚骰子,然后运行以下代码
public class Mian { public static void main(String[] args) { double ShuiGShu = Math.random * 7; if (ShuiGShu < 1) { System.out.println("1/7概率"); } if (ShuiGShu = 114514) { System.out.println("妈妈生的"); } } }发布于 2023-11-14 19:39・IP 属地浙江查看全文>>
起啥名字好 - 1 个点赞 👍
简单计算,6*6-1,选择5个数对为一组。
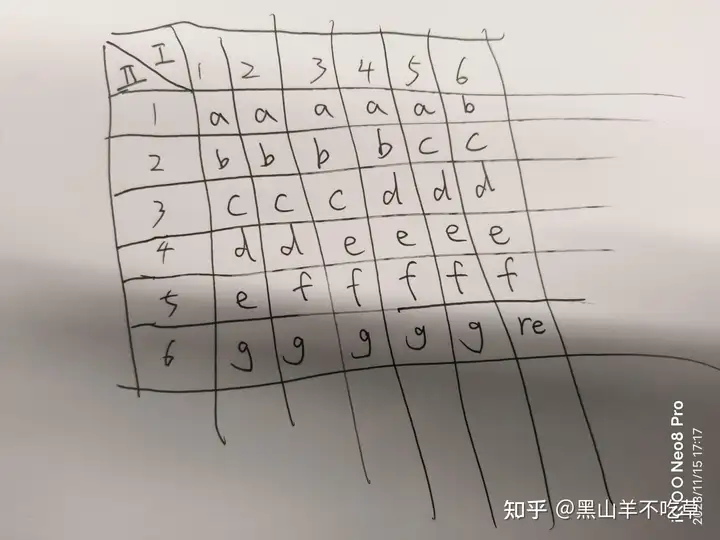
连续两个6就重新投一次,其余情况见表。
发布于 2023-11-15 17:18・IP 属地上海真诚赞赏,手留余香还没有人赞赏,快来当第一个赞赏的人吧!查看全文>>
黑山羊不吃草 - 1 个点赞 👍
可以。
考虑如下色子:
取一个高足够大的正七棱柱,在两底面各拼接一个底面大小与七棱柱底面相等的高足够大的正七棱锥,使得以七棱锥的侧面放置在地面时,体的重心的垂直投影在该侧面之外,即无法稳定立于地面。在七棱锥的七个侧面分别标号1至7。
发布于 2023-11-16 13:53・IP 属地北京查看全文>>
换什么名字好呢 - 1 个点赞 👍
这里一般性的给出模拟的概率为p时的最优构造,其中p是0到1间任意实数。
下面称“结果为A”指那p的概率的结果,“结果为B”指剩下(1-p)的概率的结果。
我们令骰子每次抛出的数字是0到5间的数。
考虑将p转换到6进制下,不妨设小数位以此为 a1,a2,a3....,其中a是0到5间的数。
若当前抛的是第k次,抛出的数字为x,讨论:
- 若x<ak,直接得到结果为A。
- 若x>ak,直接得到结果为B。
- 若x=ak,继续抛下一次,直到终止。
不难发现,得到结果A的概率恰好是p。
事实上可以证明,这种抛法,抛的次数的期望,是最小的。这边是我称它为最优构造的原因。
大家不妨试着算一算,以原题p=1/7为例,下面三种抛法的期望次数分别是多少?
- 抛两次,如果结果36种中的1~7间,按“是否为1”直接得到结论,否则再抛两次,直到成功(也就是不少答主的方法)。
- 抛两次,如果结果36种中的1~35间,按“是否在1~5间”得出结论,否则再抛两次,直到成功。
- 我的做法。
看看是不是我是最小的?
发布于 2023-11-18 00:18・IP 属地安徽查看全文>>
OvOvO - 0 个点赞 👍
查看全文>>
汪洋 - 0 个点赞 👍
查看全文>>
莫须有 - 0 个点赞 👍
我们可以考虑更一般的问题:
给定一个随机数生成器
randN, 这个方法可以生成 [1,N] 范围内的随机整数,现在我们想要使用这个生成器,来得到另一个随机数生成器randM,即能够生成 [1,M] 范围内的随机整数预处理
首先,我们可以假设 N\geq M , 如果 N<M 的话,那么我们就可以投 k=\lceil \log_NM\rceil 次来得到一个 [1, N^k] 的随机数生成器,这样问题就变成了N\geq M的形式。
我们记[1, N^k]的随机数生成器为
randNk, 注意到[1, N^k]由区间[0, N^k-1]平移一位得到, 而区间[1, N^k]可以视作一个 k 位 N 进制,这样我们就可以将randN转换为randNk, 代码如下:def randN(N): return random.randint(1, N) def randNk(N: int, k: int): x = 0 for i in range(k): x += (randN(N) - 1) * N**i return x + 1接下来,我们就可以使用拒绝采样(reject sampling)由
randNk生成randM.算法1
最简单的拒绝采样算法就是
- 从
randN中采样k=\lceil \log_NM\rceil次,将结果相乘得到 x - 如果 x\leq M , 那么采样完成;否则,跳到第一步重新采样
写成python代码就是:
def randM_from_randN1(N, M): k = math.ceil(math.log(M, N)) while True: x = randNk(N, k) if x <= M: return x我们可以来分析一下调用的次数, 记调用次数为 C , 注意到C是一个随机变量,其期望为
\mathbb{E}[C] = k*1+k\frac{N^k-M}{N^k}+\cdots+k\left(\frac{N^k-M}{N^k}\right)^i=k\sum_{i=0}^{\infty}\left(\frac{N^k-M}{N^k}\right)^i=\frac{kN^k}{M}
这里 k*1 代表我们至少要调用
randNk 次来得到一个结果,第二项代表如果我们第一次失败了(以概率 (N^k-M)/N^k ),则需要再调用 k 次。。。当 N=6 , M=7 时,我们平均需要 \lceil \log_67\rceil*6^2/7\approx 10.28 次才能成功,这显然是不能接受的。
算法2
算法1的问题是,我们抛弃了太多的值,当 N=6 , M=7 时,我们每轮拒绝的比例是 (6^2-7)/6^2=29/36 , 因此我们需要改进.
注意到区间 [1,kM] 的随机数可以变成区间 [1,M] 的随机数,这只要进行一个简单的模运算就可以了:对 x\in [1,kM] , 我们有 x\ \mathrm{mod}\ M\in[0, M-1] . 这样我们就利用了更多的数,还是以 , M=7为例,对于 [1, 28] 中的数,我们都接受,然后使用模运算得到 [0, 6] 中的均匀随机数,这样就减少了平均调用次数,代码如下:
def randM_from_randN2(N, M): k = math.ceil(math.log(M, N)) r = N**k // M while True: x = randNk(N, k) if x <= r * M: return (x - 1) % M + 1与上面的分析一样,但是现在失败的概率变成了 (N^k-rM)/N^k , 其中 r=\lfloor \frac{N^k}{M} \rfloor . 这样
\mathbb{E}[C] =\frac{kN^k}{rM}
当 N=6 , M=7 时,我们平均需要 \lceil \log_67\rceil * 6^2/(7*5)\approx 2.05 次成功,这相当于算法1显然是非常大的提升。这时,我们每轮拒绝的比例为 (6^2-7*5)/6^2=1/36 .
最后我们可以验证一下算法的正确性:
import random import math from collections import defaultdict def randN(N): return random.randint(1, N) def randNk(N: int, k: int) -> int: x = 0 for i in range(k): x += (randN(N) - 1) * N**i return x + 1 def randM_from_randN1(N, M): k = math.ceil(math.log(M, N)) count = 0 while True: x = 0 count += 1 x = randNk(N, k) if x <= M: return x, count * k def randM_from_randN2(N, M): k = math.ceil(math.log(M, N)) r = N**k // M count = 0 while True: x = 0 count += 1 x = randNk(N, k) if x <= r * M: return (x - 1) % M + 1, count * k iters = 1000000 counts = [] result = defaultdict(int) for _ in range(iters): x, count = randM_from_randN1(6, 7) # x, count = randM_from_randN2(6, 7) counts.append(count) result[x] += 1 print(sum(counts) / iters) print(result)分别运行算法1和算法2 1000000 次得到的结果如下:
# randM_from_randN1 10.296348 defaultdict(<class 'int'>, {4: 142374, 7: 142717, 5: 142928, 2: 142686, 6: 143172, 1: 143148, 3: 142975}) # randM_from_randN2 2.05696 defaultdict(<class 'int'>, {7: 142504, 2: 143050, 3: 142237, 4: 142711, 1: 143311, 5: 143193, 6: 142994})发布于 2023-11-14 19:46・IP 属地上海查看全文>>
吾往矣 - 从
- 0 个点赞 👍
可以啊,这个骰子像一根铅笔,两头削尖。
区别在于普通铅笔的截面是正六边形的,这个像铅笔的骰子横截面是正七边形的
你扔嘛,每面1/7的概率
其它面数也都可以这么做。
发布于 2023-11-14 19:20・IP 属地英国查看全文>>
NaHCO3 - 0 个点赞 👍
查看全文>>
dolphin625 - 0 个点赞 👍
查看全文>>
ts li - 0 个点赞 👍
提供一个不用舍弃任何结果、且每掷一次就试验一次的方法。
第 n 次掷骰子时,获得 \left[ 1, 6 \right] 范围内的一个随机整数 r,记 S_{n}=S_{n-1}+r(令 S_{0}=0)。如果 S_{n} 除以 7 的余数为 0,则认为事件发生。
改进: S_{n}=S_{n-1}+K\cdot r+B ,其中 K 和 B 是常数。通过恰当地设置这两个常数,可避免已知上一次发生可推导下一次必然不发生,以及首次必然不发生的问题。
理论解释:虽然看起来每次试验都跟上一次试验相关,但由于存在掷骰子这个随机行为,所以结果仍然是随机的。
下面是一个模拟程序,测试这个方法的效果。
int N = 100_000_000; int K = 2; int B = 5; long S = 0; int c = 0; for (int n = 1; n <= N; n++) { S += K * Random.Shared.Next(1, 7) + B; if (S % 7 == 0) c++; } Console.WriteLine(c / (double)N);运行 3 次结果为:0.14285887,0.14274658,0.1428576。(1 / 7 = 0.142857)
编辑于 2023-11-14 22:46・IP 属地四川查看全文>>
YY-GamePlayer - 0 个点赞 👍
查看全文>>
乂二 - 0 个点赞 👍
查看全文>>
冷情 - 0 个点赞 👍
只要可以多次投掷就可以啊。
经典随机算法:
投掷两次有36种组合,选35种分配给1-7, 剩下一种重新再投一组。
可能会有人认为这个重新投掷有没有可能一直重投。事实上,这个收敛速度非常快。一次投不出结果概率为 1/36,两次还不出结果概率平方,三次不出结果需要这个概率立方。
所以获得一次有效投掷,需要投几组两次?数学期望上是 36/35 组。
发布于 2023-11-15 07:50・IP 属地美国查看全文>>
大尾巴狼