数学是人类的发明，还是发现？
- 47879 个点赞 👍
讲真，对这个问题感兴趣，还点进来看的人，都不是一般人。
^_^简单的说，早期的古代数学多数是发现，但是从2000多年前的古希腊开始，数学家们创造出大量超越自然的新事物，导致此后的数学越来越多的是发明。
文艺复兴三杰拉斐尔的名画《雅典学院》图片出处：https://commons.wikimedia.org/wiki/File:La_scuola_di_Atene.jpg古希腊的先贤们也不会想到，他们居然为人类开辟出一片新的世界。
在这个新世界中，人类的思想得到了前所未有的解放，并加速了科学与技术的进步，让人类文明进入了快速腾飞的时代。
一切先从定义开始数学究竟是发现（discovered），还是发明（invented），取决于「发明」和「发现」的定义。
先看两个案例：科学家发现了微观粒子，而不是发明了微观粒子；殷商时代的古人发明了甲骨文，而不是发现了甲骨文。
通过这个例子，我们可以达成共识：发现，是指人类在自然宇宙里找到了以前没见过的事物发明，是指人类创造出了自然宇宙中以前不存在的事物如果以这两个定义为基础，可以推出：因为，数学的定义、符号和规则都是人类的发明，是自然宇宙中以前不存在的事物。
所以，数学是人类的发明，而不是发现。
Q.E.D.等一下，这样就证明结束了吗？并没有，因为事情没有这么简单。
有限的自然宇宙和无穷的数学宇宙无穷符号「无穷」是数学中最核心的概念之一，但是「无穷」只存在于人类的想象中，不存在于自然宇宙中。
在我们的印象里，自然宇宙是无穷的。
然而，随着人类观测能力的增强，天文学家逐渐发现，越来越多的证据表明，宇宙是有限的，我们所生活的自然宇宙，实际上比我们想象的要「小」的多。
天文学家是如何发现宇宙是有限的，这是一段很有趣的历史，篇幅原因不在这里展开，推荐一部精彩的BBC纪录片《万物与虚无》(Everything and Nothing)，非常通俗和系统的介绍了这段历史，你可以在B站上找到。
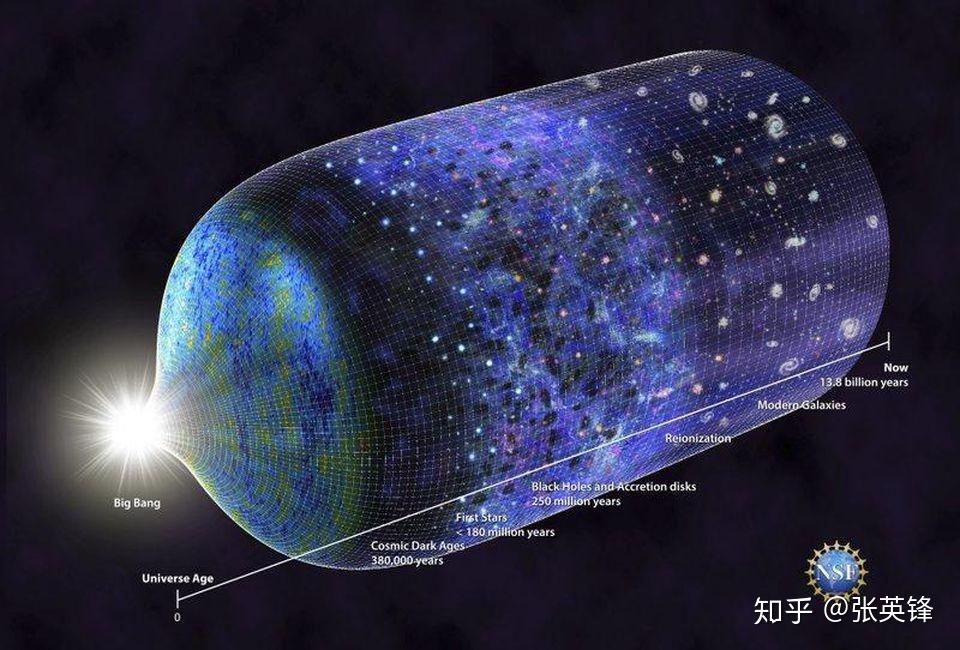
BBC纪录片《万物与虚无》(Everything and Nothing)根据天文学家观测到的天文数据，科学家发现宇宙的时间不能无限上溯，而是存在一个叫「大爆炸」的起点，宇宙的年龄估计不超过200亿年；宇宙的空间也非无限，宇宙的直径不超过1000亿光年；而宇宙里所有普通物质的质量是1.45×10^{53}1.45×10^{53} 千克，尽管这些都是极其庞大的天文数字，但也是有限的。
[1]也就是说，我们印象里那个无穷的宇宙，是我们想象出来的。
宇宙中所有已知的自然事物，包括时间、空间、物质、能量……等等都是有限的，在自然中并不存在无穷的事物。
图片出处：What Really Put The 'Bang' In The Big Bang?然而，相比于自然，在数学的世界里，无穷几乎无处不在。
简单的，如分数1/3，就可以表达为无限循环小数0.3333……常见的，如圆周率π，则是一个无限不循环的常数，这个数就蕴含着无穷。
圆周率π图片出处：How to make the digits of π go around in a spiral like this?人类至今也无法穷尽圆周率的计算，并不是因为它难算，而是因为人类所拥有的能量和物质是有限的。
不要忘了，无论是电脑，还是人脑，在计算时都需要消耗能量和时间，而存储数据时，也要占用物质和空间，所以人类的算力不能无限的增长。
事实上，即使人类穷尽宇宙里所有的能量，即便计算到宇宙毁灭，也无法计算出圆周率的最后一位；即便耗尽所有的物质，写满了宇宙所有的空间，也无法把圆周率计算的数据保存下来。
因为无穷是没有尽头的！请仔细想想，是不是这样！仅仅是数学世界中一个常见数字的计算，就可以耗尽我们这个自然宇宙中所有的能量、物质、时间和空间。
有趣的是，数学家还证明了，像π这样的无理数，其个数要远远多于有理数。
更有趣的是，有的无穷比另外一些无穷还要大，比如说自然数的个数有无穷多个，而实数的个数却远比自然数多的多。
这些无穷，都是人类在数学世界里证明和创造出来的新概念，它们在自然宇宙中并不存在，是人类在对自然宇宙观察和思考后，在数学世界中重新发明的新事物。
换句话说，数学世界和自然世界是截然不同的两个世界，数学是人类创造出来的全新世界[2]。
无穷让数学凌驾于其他科学之上公元前6世纪，古希腊人证明出了第一个数学定理，从此，无穷进入了数学。
第一个定理是泰勒斯证明出来的泰勒斯定理，和他同时代的毕达哥拉斯则证明了勾股定理，并建立了第一个数学学派。
《雅典学院》中的毕达哥拉斯，旁边抄作业的是德莫克里克（维基百科说图中抄作业的是阿那克西曼德，但他比毕达哥拉斯要早，我更倾向于是德谟克利特，反正拉斐尔也没明确他是谁）毕达哥拉斯用逻辑推理的方式，证明了直角三角形都遵循勾股定理。
这里针对的「直角三角形」并不是指某一个直角三角形，而是指所有的直角三角形，对无穷多的直角三角形都成立，不存在例外。
正是因为毕达哥拉斯的这个贡献，他和泰勒斯都被戴上了「第一位数学家」的桂冠。
在他们之前的古巴比伦、古埃及的数学家，都无法获得这个殊荣，尽管他们提前一两千年就发现了这些定律，但是他们并没有把定律证明成定理。
（当然很可能他们也证明了，只是还没有足够的证据支持）是无穷让定律和定理之间产生了天壤之别。
定律是对已知规律的归纳总结，将来可能会出现例外情况，改写定律。
而定理则通过演绎推理实现了无穷，不存在例外情况，不会被推翻。
所以，毕达哥拉斯之前的古代数学家更多的是发现，他们发现了很多定律，但是没有发明太多超越自然宇宙的数学概念。
而毕达哥拉斯之后的数学家，引入了演绎和无穷，还定义了很多超越自然的概念，导致此后的数学越来越多的是发明。
这是一个历史性的时刻，古希腊哲学家开辟了一个无穷的新世界，而数学也从此开始凌驾于其他科学之上。
高斯称，「数学是科学的皇后」（Regina Scientiarum）。
而爱因斯坦也表示认同[3]数学之所以拥有超越其他所有科学的地位，是因为数学中的法则是绝对确定和无可质疑的，而其他科学的法则则是可质疑的，并随时有被新发现的事实所推翻的危险。
One reason why mathematics enjoys special esteem, above all other sciences, is that its laws are absolutely certain and indisputable, while those of other sciences are to some extent debatable and in constant danger of being overthrown by newly discovered facts.大部分自然科学中的定律，放在数学中只能算作猜想。
因为这些定律都是观察、归纳而来的，还不能靠严格的证明保证其永远成立。
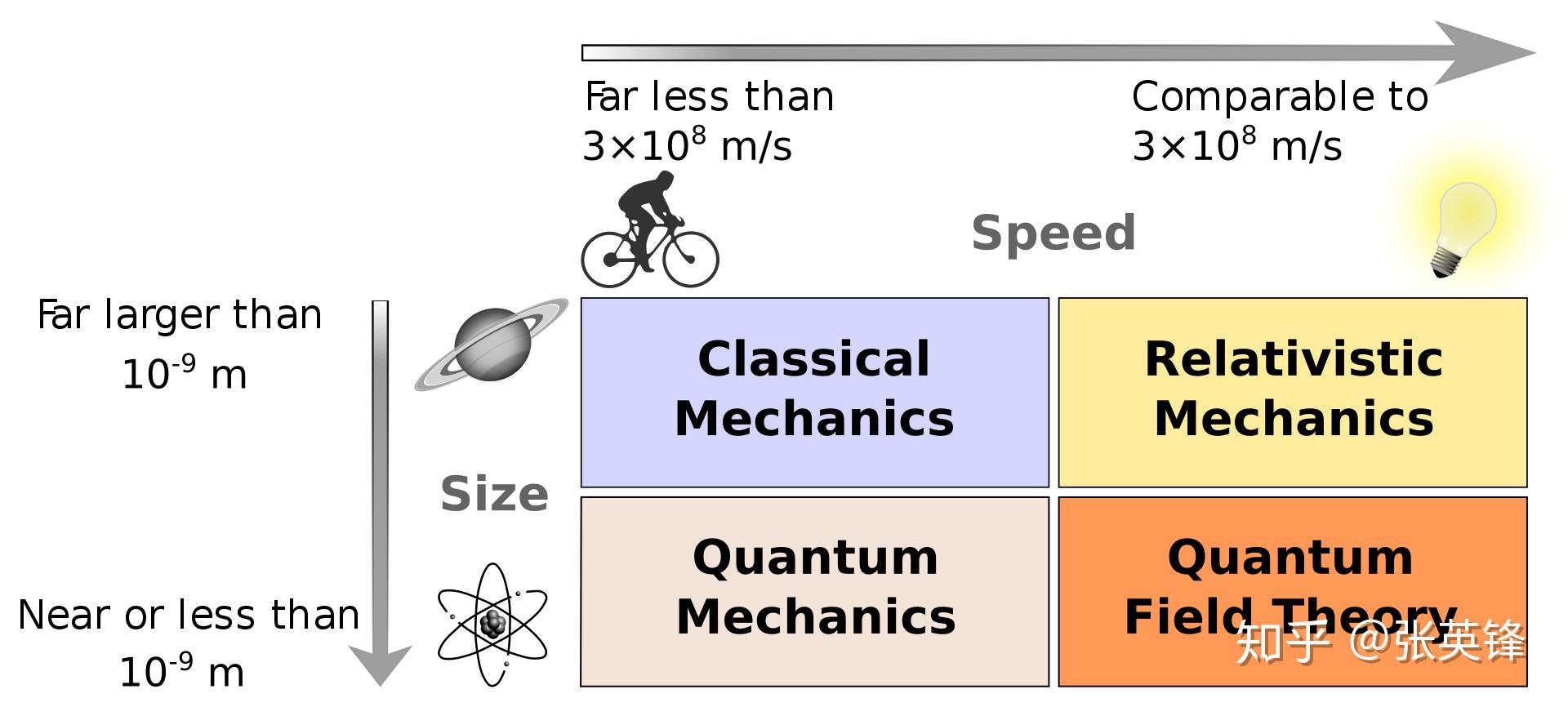
例如以牛顿定律所构建的经典力学，后来就被相对论和量子力学所改写。
现代物理学图片出处：https://en.wikipedia.org/wiki/Modern_physics数学的地位要归功于无穷，数学家赫尔曼.外尔（Hermann Weyl ）也说[4]：数学被称为关于无穷的科学。
的确，数学家发明了有限构造，通过该构造可以解决问题，而其本性却隐含着无穷。
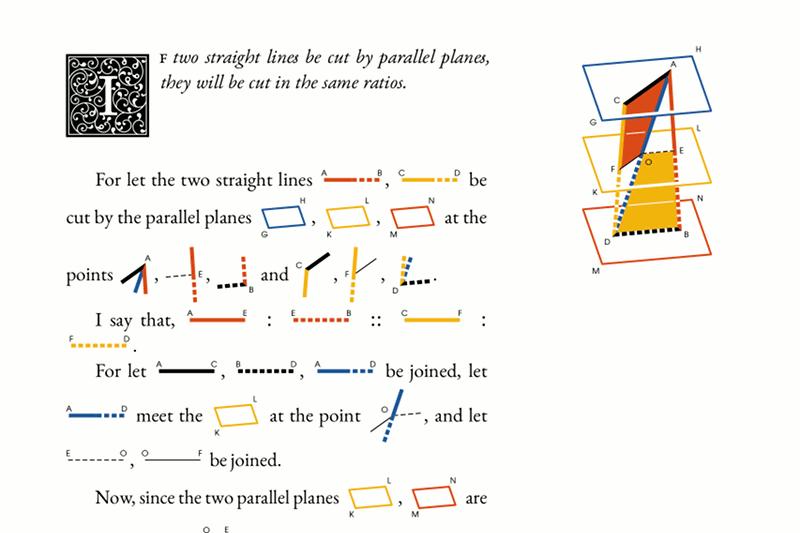
Mathematics has been called the science of the infinite. Indeed, the mathematician invents finite constructions by which questions are decided that by their very nature refer to the infinite. 外尔的第一句话，我们已经理解，第二句话也很重要，可是该如何理解呢？让我们以《几何原本》为例：利玛窦和徐光启所翻译的拉丁语版《几何原本》图片出处：Mathematical Treasures - Christopher Clavius's Edition of Euclid's Elements古希腊数学家欧几里得的《几何原本》，是数学史上最重要的文献之一，这本书的第一句话就暗含了无穷。
定义1. 点：点无法再分割成部分。
Definition 1. A point is that which has no part. 有没有意识到，这个定义很古怪，但是哪里古怪，又说不出来。
其实，这是欧几里得在用精巧的话术，想方设法的要绕开无穷，只是为了说明「点」只有位置，而没有大小。
如果直接说「点」没有大小，就必须引出「无穷小」这个至关重要的概念。
所谓「无穷小」是指无限的接近于零，却不等于零。
古希腊人发现「无穷小」会引发很多悖论，他们无法解决，所以只好用「分割」来定义「点」，回避「无穷小」悖论。
如果有人问：你这个定义是不是包含了无穷小？！那就可以反驳：谁说无穷小了？我说的是「不能再分割」。
不管怎么说，无穷隐含其中。
有趣的是，无穷小悖论要等到2000多年后才得到解决，方法之一也是「分割」。
这里有很多有趣的故事，将来有机会再详细展开深谈。
另外，这种没有大小的「点」，是人类头脑中想象出来的。
不仅古希腊人从来没有在自然中发现过，就是我们现代人也没有见过。
几何中的「点」是一种超越自然的事物，是欧几里得在另一位古希腊哲学家——德谟克利特——发明的原子论的基础之上，创造出来的数学概念。
《雅典学院》中手拿圆规作图的欧几里得，定义完了「点」，紧接着，欧几里得又在「点」的定义基础之上，构造出了「线」的定义，定义2．线：线是没有宽度的长度。
定义3．线的两端是点。
定义4．直线：直线是线上的点均匀平直的分布。
Definition 2. A line is breadthless length. Definition 3. The ends of a line are points. Definition 4. A straight line is a line which lies evenly with the points on itself.有了「线」的定义，接下来是「面」的定义，然后是各种「几何图形」的定义，……欧几里得构造了点、线、面、形、角等23个数学元素的定义（后面的12卷又增加到了131个），以及5条公理、5条公设，并以这些有限的元素和规则证明了465个命题，构建出无限的欧几里得几何空间。
号称最美的彩版《几何原本》中的插图图片出处：Making of Byrne’s Euclid数学的定义里有无穷、定理里也有无穷、数学的空间也是无穷的……，总之数学世界中到处都是无穷。
回过头来，再重新品味外尔的话的确，数学家发明了有限构造，通过该构造可以解决问题，而其本性却隐含着无穷。
是不是容易理解了？数学来源于自然，却高于自然。
人类观察鸟的飞行，发现了飞行的原理，然后发明出飞机这种全新的事物。
随着人类对飞机的不断改良，飞机的速度和范围很快就超越了所有鸟类。
同样的，数学中的元素和规则也是人类观察自然，发现了自然中的规律，然后重新发明出来的新事物，这些新事物在自然宇宙中并不存在。
随着几千年来，数学家的不断构造和完善，数学宇宙的边界早已经超越了自然宇宙的边界。
所以，数学并不是自然的一部分，而是在自然之外的另一套新事物重新组成的集合，数学已经自成体系，超越了自然宇宙。
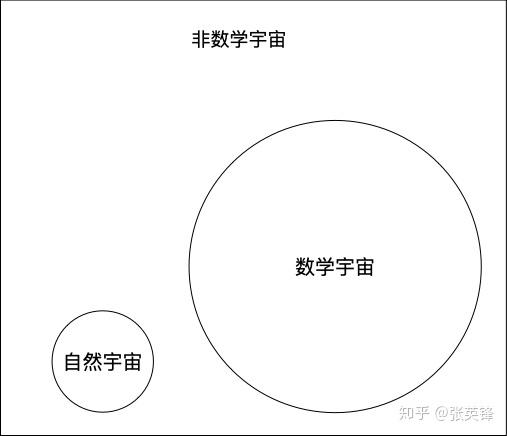
正是因为人类发明了无穷，发明了数学符号和运算规则，所以数学宇宙的空间远远大于人类所生活的这个自然宇宙。
数学的计算边界远远超过自然注意，这个图只是演示数学可计算的空间远远超出了自然宇宙的范围，并不代表数学已经比自然大。
数学完全有能力来描述我们所在的这个自然宇宙，但是反过来，数学宇宙中的很多东西是无法用自然事物来描述的，比如无穷。
这是不是很神奇？爱因斯坦也这样认为，他说[6]宇宙的可理解性是宇宙永远的秘密......宇宙居然能被理解，这个事实本身，就是一个奇迹。
The eternal mystery of the world is its comprehensibility … The fact that it is comprehensible is a miracle.而我们之所以可以理解宇宙，必须要归功于数学。
20多万年前，当智人出现在非洲大陆时，此时的智人大脑已经和现代人相差无几，但那个时候的人类根本无法理解宇宙。
此后的20万年里，绝大多数时间，人类也无法理解宇宙。
直到最近的500年，直到人类发明了代数、微积分等现代数学，我们才算真的理解宇宙。
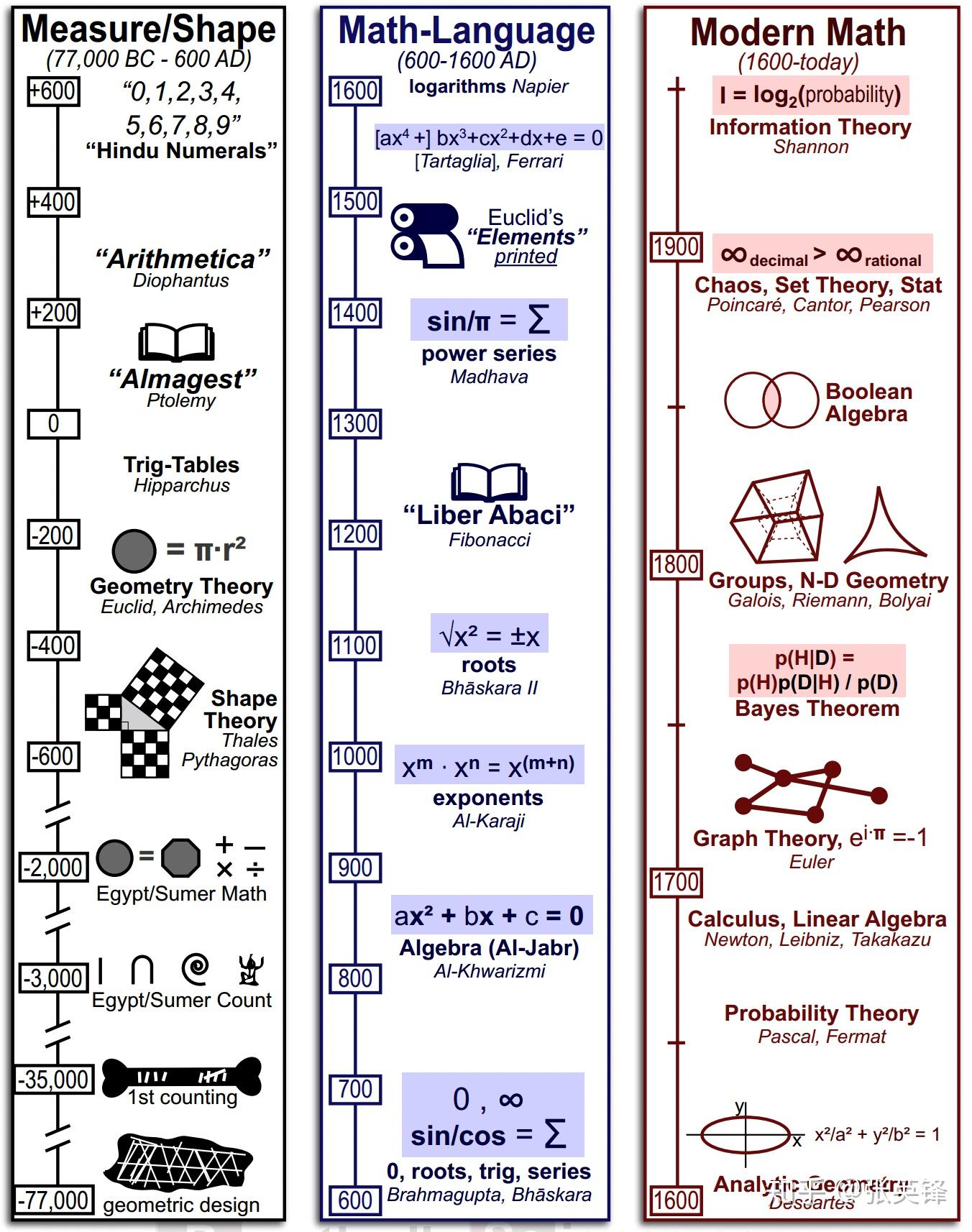
数学史的时间线图片出处：https://www.practicallyscience.com/a-history-of-math/按照数学史的时间线：5000多年前，人类发明出算数计算2000多年前，古希腊人发明了几何证明400多年前，欧洲人发明了代数和微积分100多年前，数学家建立起了现代数学体系直到此时，爱因斯坦才有能力用现代数学的强大工具发明出了相对论，如果没有现代数学，即使爱因斯坦也寸步难行。
是数学让爱因斯坦强大，而不是天赋这个图片是搞笑用的，但内容是认真的，是数学让爱因斯坦强大，而不是大家津津乐道的智商和天赋。
一个不会现代数学的爱因斯坦，和一个掌握现代数学的爱因斯坦，只有后者才可以发明相对论。
智商决定不了人的上限，是人所能掌握的数学水平，限制了人能掌握的科学和技术水平，而这些才决定了人的上限。
事实上，数学家每发明创造出一个新的数学概念，都会让数学的边界扩展出一个更庞大的无穷空间。
如果只依靠发现的话，数学家的能力就会受到极大的限制。
2000多年前，毕达哥拉斯学派的希帕索斯，基于勾股定理发明出了根号2，这种不能用自然数的比例（ratio）来表示的非比例数（irrational numbers），也就是无理数。
学派认为他发明出的新数，不是自然宇宙中存在的数，是亵渎神灵的行为，于是淹死了希帕索斯。
如果数学家停止脚步，只使用自然数，而不使用发明出来的新数，那就极大约束他们的能力，就不会有后来高度繁荣的数学世界了。
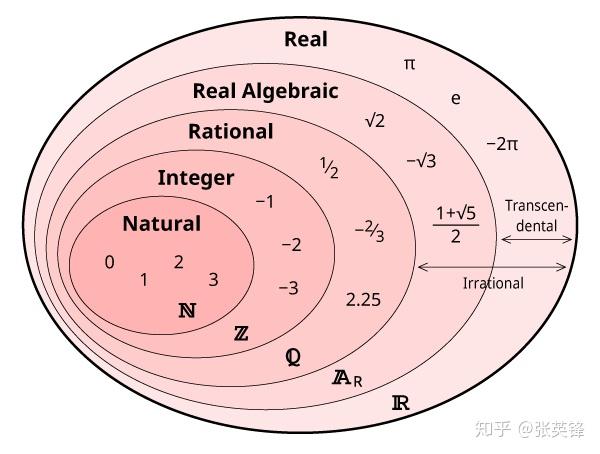
经过2000多年创造，数学家打破了自然的限制，发明出了越来越多自然宇宙中并不存在的新数。
图片出处：Number Sets而现代人正是使用负数、无理数、虚数（imaginary number）……等这些数学家发明的数学概念，才能让我们计算的边界远远超出古希腊人的想象。
到目前为止，我们讨论的还只是数学在尺度上的无穷，不要忘了，数学还可以让维度无穷。
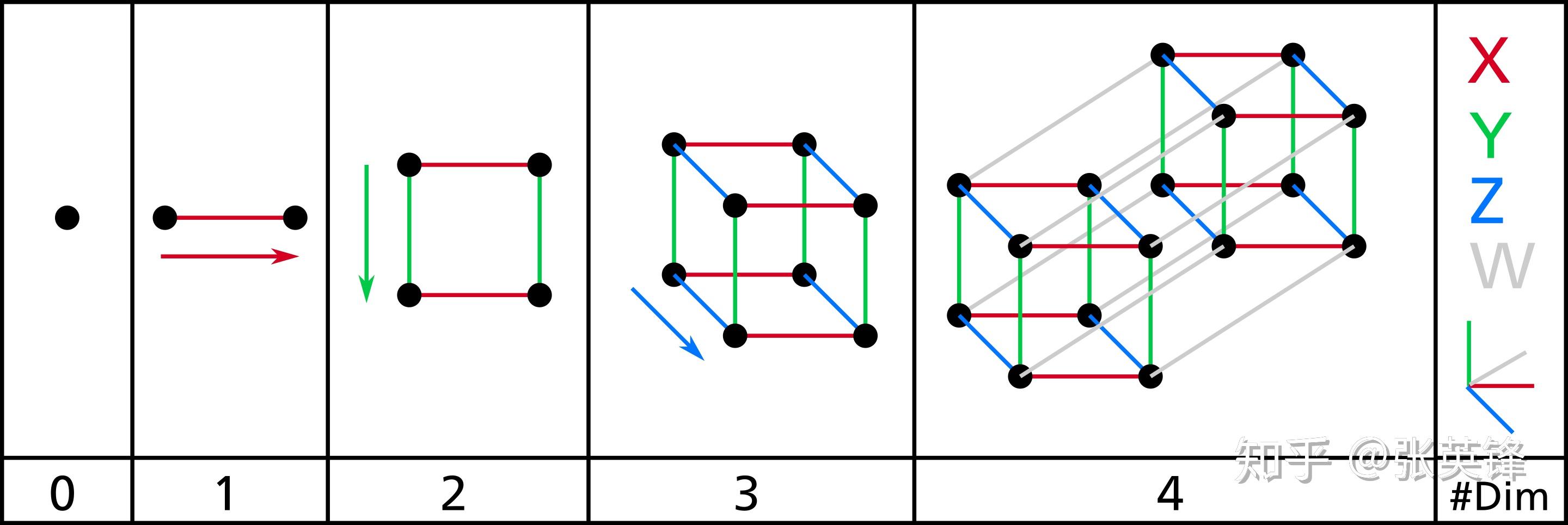
从0维空间到4维空间图片出处：https://en.wikipedia.org/wiki/Tesseract我们的自然宇宙，是三维空间，再加上一维时间所构成的四维时空。
然而，数学家却可以创造出五维、六维……以至于无穷维度的，任意高维的空间，这些发明出来的高维空间在自然中当然也是不存在的。
物理学家费曼就有个《数学和物理关系》的演讲，说的就是数学家总是把定理推广到无穷维空间，而物理学家却只需要三维空间，非常的搞笑，推荐你看一下[6]。
可怜的物理学家总是要回来，再向数学家请教更高维的情况自然宇宙是一个空间有限、维度有限的宇宙；而数学则可以创造出空间无限、维度无限的宇宙，这些宇宙的数量也可以是无穷多个。
在《三体》中，歌者用二向箔把太阳系碾压成低维空间，以降维打击彻底毁灭了地球文明，这是高级文明对低级文明的强大优势。
二向箔把太阳系碾压成低维空间图片出处：《三体艺术插画集》而如果能让数学家把数学工具带到自然宇宙的话，他们完全可以碾压歌者，彻底摧毁歌者文明。
如果想限制住数学家的力量，就让他们只能用在自然中才存在的事物。
这样人类的科学探索能力，就会被永远锁死在2000多年前的古代，这比智子锁死基础物理还要狠毒！(三体迷都知道的梗^_^)幸好，数学家已经摆脱了自然的限制，就像《西游记》里的孙悟空一样，『跳出三界外，不在五行中』，这是前所未有的自由。
『人定胜天』这个梦想，至少在数学上已经完全实现了！现在你已经明白了，数学的强大力量恰恰来自于发明，而没有停留在发现上。
数学是人类文明对自然的伟大超越！数学不是自然科学，而是形式科学数学超越了自然，也超越了以自然为研究对象的自然科学，所以数学不是自然科学。
物理学、化学、生物学这些自然科学，他们的所有概念都来自于自然宇宙，不能超越自然宇宙。
而数学中却有很多超越自然宇宙的事物，例如无穷等。
另外，我们也知道数学是科学，因为数学和其他科学一样，能提供确定性，是可重复的、可验证的。
例如，同一个定理，所有人都可以重复验证其证明过程，得出相同的结论。
所以，我们把数学这种类型的科学归类于形式科学（Formal science）。
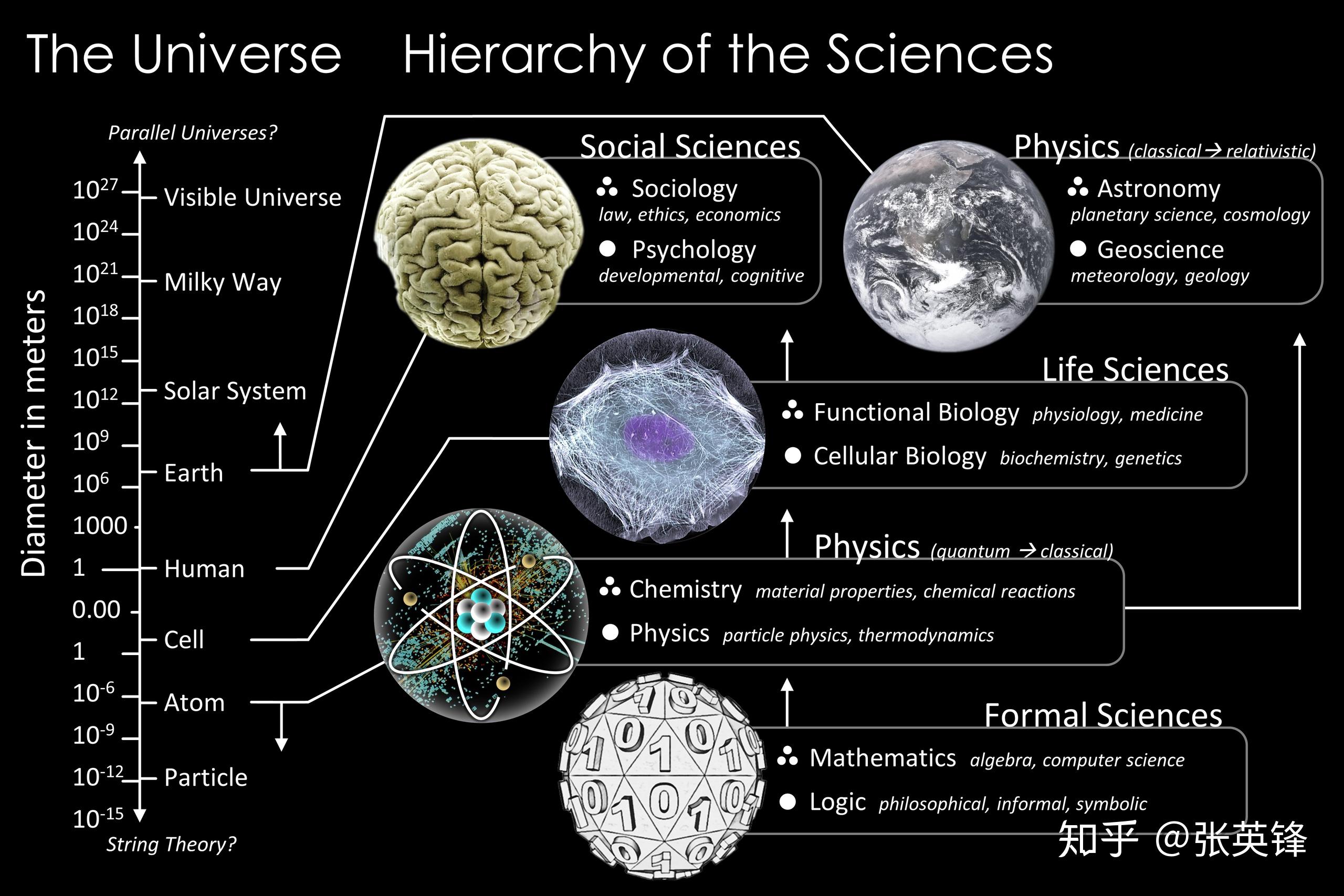
这张图就展示了形式科学和自然科学、社会科学等其他科学的关系。
科学的层级结构图片出处：https://en.wikipedia.org/wiki/Hierarchy_of_the_sciences从图中，你可以看到，形式科学虽然不属于自然宇宙的范畴，却处于所有科学的最底层。
数学为物理学和化学等提供了坚实的基础，而物理学和化学又为生命科学提供了的基础，最后生命科学又为社会科学提供了基础，这是一个自下而上的层级结构在拉斐尔的《雅典学院》中，如果仔细观察就会发现画中暗藏着一个金字塔形的层次结构。
整个《雅典学院》以柏拉图和亚里士多德为中心，同时他们也是身边人物的视线焦点。
如果以亚里士多德伸出的右手作为顶点，可以做出一个等腰三角形，从台阶之上向下延伸到地板，底边的两个角右边指向毕达哥拉斯，左边指向欧几里得。
注意观察，就会发现这两个数学家也是周围人物的视线焦点。
拉斐尔用这样的构图来表达，在自然哲学的层级结构中，数学是整个自然哲学的基础。
在《雅典学院》这幅画里，拉斐尔还有很多有趣的心机，将来再给大家逐一揭秘。
可是以数学为代表的形式科学为什么能够成为自然科学、社会科学的基础呢？回答这个问题，就必须理解形式科学是什么？什么是形式科学？更关键的是，什么是形式（Form）？如果你去搜索和查阅，就会发现很多类似于形式逻辑、形式语言、形式系统……等各种不明觉厉的抽象概念。
比如维基百科对「形式」的解释：[7]形式（英语：Form）是一个在古希腊哲学中的重要概念。
其与质料相对应，描述了事物的本质，指“第一实体”。
看完是不是仍然一头雾水，形式到底是个啥啊！？可继续写下去，就超越了本文的主题，篇幅太长也不利于阅读。
我会再写一系列的文章，用通俗易懂的语言，让大家理解形式科学，同时也解答本文中没有回答的问题：为什么形式科学能够成为自然科学、社会科学的基础？物理、化学中的符号也是人类的发明，难道物理、化学也是发明？人的大脑为什么能创造出超越自然的事物？数学中超越自然的力量是什么？科学究竟是什么？……我都会在以后的文章中回答。
敬请关注！总结本文是从拉斐尔的名画《雅典学院》开始的，所以也用这幅画来结束。
在《雅典学院》壁画的中央，站立着柏拉图和亚里士多德。
《雅典学院》中的C位，柏拉图和亚里士多德右边是由达芬奇Cosplay的柏拉图，他的右手竖着中指（啊不，是食指）指向天空，左手夹着《蒂迈欧篇》，象征着「形式」可以构造出理想的世界。
左边是亚里斯多德（可能是米开朗基罗Cosplay），右手拍向大地，左手扶着《伦理学》，象征着「经验」需要通过脚踏实地的观察才能发现。
他们两个人，正好代表了人类获得知识的两种途径：一种来自演绎、发明，另一种则来自归纳、发现。
我们都知道，两者不是非此即彼的关系，而是兼而有之的关系。
但本文的主题『数学是人类的发明，还是发现？』，却让人不由自主的想做「二选一」，这是「二元论」的天然特性。
至于为什么人类会有这种倾向，也是一个好问题，我们在下次讲形式科学的时候会分析。
警惕「二元论」的陷阱「二元论」会让人的注意力带宽变窄。
如果有人问你：你想喝咖啡，还是喝茶？大部分人的注意力都会集中这两个选择上，在「咖啡」和「茶」中二选一。
Coffee or Tea?但少数人会注意到，我们其实有无穷种选择。
可以选择喝免费的冰水也可以选择什么都不喝或者选择茶、咖啡之外的任何一种饮料……再比如：人是「孩子」，还是「成人」？小时候是孩子，长大了就是成人，「孩子」和「成人」也不是非此即彼的关系，只是代表了同一个事物、不同的阶段。
对数学也是同样如此，发现和发明也是数学的不同阶段：数学家观察自然，在数量和图形中发现了数学规律数学家根据发现，设计出新的数学元素，并通过演绎引入了无穷无穷将自然定律变成了数学定理，数学逐渐开始超越自然数学家发明出大量新的数学元素和规则，开拓出一个又一个的数学无穷宇宙人类借助数学宇宙中超越自然的力量，实现了科学、技术的大繁荣数学起源于自然，独立于自然，超越了自然，最终演化为一个全新的世界所以，发明和发现在过程上是统一的，并非对立。
Is math discovered or invented?你看漫画里的这个人，是不是成功跳出了二元论，思维更自由了！^_^开个玩笑。
解决问题时，更好的技巧是对复杂的事物推迟使用二元论，尽可能多的使用拆解和分析，慢慢的，真相就能浮出水面。
这种方法也是所有科学最重要的方法之一，将来一定要展开了介绍。
如果用一句话来总结这篇文章的意义，那就是：把数学从自然中分割出来，变成了一个独立的世界。
以前我们总是将两者混在一起讨论，造成了各种混乱，分离之后就清晰多了。
在后面我们介绍形式科学的时候，你会发现这样分割的巨大好处。
在本文的开头，我提到过，对这个问题感兴趣，还点进来看的人，都不是一般人。
而能坚持到这里的人，我相信更是寥寥无几。
别忘了给自己，也给这个答案点个赞，留作纪念！One More Thing：这篇文章和接下来的系列文章，都会在我的微信公号上发布，最后将集结成册，汇编为一本迷你电子书，供大家免费下载，书名暂定为《形式宇宙》。
敬请关注我的微信公号：zyfedu最后，给大家分享一本数学电子书。
关注我的微信公号zyfedu，在私信中发送：几何原本就可以获得文章中提到的最美彩版《几何原本》的PDF电子版。
1847年，爱尔兰工程师Oliver Byrne出版了一套非常惊艳的《几何原本》，全书的插图全部采用彩色印刷，颠覆了传统几何书籍灰暗单调的风格。
[8]图片出处：Making of Byrne’s Euclidhttp://c82.net网站对该书做了数字修复，并制作了可交互的在线《几何原本》，强烈建议大家去体验一下。
上海三联书店也出版了该书的纸质版，售价高达400多元，土豪请无视高达二字。
我在微信号zyfedu上分享的PDF文件，是俄罗斯人Sergey Slyusarev用ConTeXt制作的前六卷。
[9][10]该电子书的许可协议是CC-BY-SA 4.0 ，你也可以在Github上找到该书的ConTeXt源代码以后我还会分享更多的公版科技图书给大家，敬请关注。
关于本文的分享和转载须知欢迎个人分享和转发本文链接，你的点赞和分享对我很重要！媒体、自媒体转载，请获得本人授权，注明作者和出处。
参考资料https://en.wikipedia.org/wiki/Observable_universe洪万生教授的讲座《数学是发现，还是发明？》视频 https://www.youtube.com/watch?v=brGqGEBnqyc&t=4984s ，文字稿【探索10 】數學是發現，還是發明？Weyl, H. Axiomatic versus constructive procedures in mathematics.The Mathematical Intelligencer 7,10–17 (1985). https://doi.org/10.1007/BF03024481Albert Einstein(1923). "Geometry and Experience".Sidelights on relativity. Courier Dover Publications. p. 27.Reprinted by Dover (2010), ISBN978-0-486-24511-9.Andrew Robinson. Did Einstein really say that? Nature 557, 30 (2018). https://doi.org/10.1038/d41586-018-05004-4【费曼物理学2-5】费曼趣谈数学家与物理学家的区别_哔哩哔哩 (゜-゜)つロ 干杯~-bilibilihttps://zh.wikipedia.org/wiki/%E5%BD%A2%E5%BC%8F_(%E5%93%B2%E5%AD%B8)https://en.wikipedia.org/wiki/Oliver_Byrne_(mathematician)https://habr.com/ru/post/451682/我如何用TeX“复活”两千多年前的《几何原本》？ - 云+社区 - 腾讯云编辑于 2021-05-19 01:47真诚赞赏，手留余香赞赏35 人已赞赏赞同 4.7 万1,557 条评论分享收藏喜欢收起。
查看全文>>
张英锋
- 9 个点赞 👍
就我的经验，是发现。
我发现陈必红定理，是在一个凌晨两点多钟惊醒，立即爬起来，做了几道题，发现是对的，一阵狂笑，觉得鲜花啊掌声啊美女啊院士啊都在向我招手，结果到了今天，啥也没有。
发布于 2021-08-03 23:32真诚赞赏，手留余香赞赏还没有人赞赏，快来当第一个赞赏的人吧！赞同 96 条评论分享收藏喜欢收起。
查看全文>>
陈必红
- 4 个点赞 👍
都有。
比如勾股定理是发现，发现了直角三角形有这个性质。
但很多定义都是发明，人们发明了这些定义，简化了表述和证明。
特别是无穷的发明，连续统的发明等，使数学严谨化了。
发布于 2021-01-02 12:35真诚赞赏，手留余香赞赏还没有人赞赏，快来当第一个赞赏的人吧！赞同 4添加评论分享收藏喜欢。
查看全文>>
babyquant
- 1 个点赞 👍
圆是发现，辅助线与坐标系是发明。
发布于 2020-12-31 00:03赞同 1添加评论分享收藏喜欢。
查看全文>>
Burgundian
- 1 个点赞 👍
发现规律的。
得感谢印度人发明了阿拉伯数字。
发布于 2021-01-02 10:24真诚赞赏，手留余香赞赏还没有人赞赏，快来当第一个赞赏的人吧！赞同 1添加评论分享收藏喜欢。
查看全文>>
超级大笨狼
- 0 个点赞 👍
看把数学当做什么。
作为思想体系的数学完全是发明，发明出来居然还可以这么想事情。
比如说，把集合作为数学基础是康托尔发明的想法。
康托尔这个世界上最可敬的神经病，脑袋里的灯泡突然就亮了，他知道这样想是可以的。
而作为命题集合的数学，那么其中的公理属于规定的范畴，规定属于发明的范畴。
定理属于发现的范畴。
而所有尚不知真假的命题的范畴也同样无法判定。
编辑于 2023-03-14 22:55・IP 属地上海赞同添加评论分享收藏喜欢。
查看全文>>
查勃多得了如是说