题主如果不是来反串或钓鱼的话,建议不要再看这种“妄史论”。对历史的全面了解应该建立在各方文献的考证,包括传世文献与最新出土文献,考古证据等等,学界论文也需多查阅,很多以前广为流传的结论在新的考证和研究下不断被证伪或更新,有部分确实还未进入教科书或通常的学史科普书,从学界到大众需要一些时间。
比如国际数学史最近二十年的主要成果之一即蓝丽蓉与洪天赐教授合著的《雪泥鸿爪溯数源》,详细严谨的论证了中东与印度在巴格达前的古代数学至今未发现十进位数符,综合多种证据提出阿拉伯数字体系的十进位制及运算体系源于中国古代筹算,推翻了早期广泛流传的印度源头论,得到世界公认。
2002年,蓝丽蓉因其在数学史领域的杰出成果,荣获数学史最高荣誉:国际数学史学会颁发的凯尼斯·梅奖,她是第一位亚洲人和第一位女学者获此殊荣。蓝丽蓉还荣获2005年新加坡大学颁发的杰出科学校友奖。相关介绍还可参考附录。
〇的历史前答有过考证,引部分相关来参考:
欧洲在古代由于采用的是繁琐冗长的罗马数码,以至于当时杰出的数学工作者,都视当今小学生已十分熟练的三位数乘以一位数为一件麻烦的事情。数学史中记载了当时算术教科书中的一个乘法事例, 计算235×4。其中235 表示为C C Ⅹ ⅩⅩ Ⅴ,4 表示为Ⅳ,C C Ⅹ Ⅹ Ⅹ Ⅴ乘以Ⅳ的算法要经过复杂的过程才能得到结果DCCCCXL (XL 是40)即940,这只是乘数为1 位数的情形,若乘数为多位数的话就更为复杂。据文献考证在当时称三位数乘三位数为世间最麻烦的事情…
中国发明的十进位制在对外交往中,东传韩国、日本,南传越南等东南亚国家;丝绸之路开通后,又传南亚、中亚等国。古代印度于公元7世纪左右才受中國影響系统改用十进位值制, 在8世纪传至古代阿拉伯, 9世纪由古代阿拉伯再传至欧洲,15世纪末、16世纪早期由欧洲传至美洲,以后又传入非洲、大洋洲。……
16世纪时,欧洲才逐渐采用按逆时针方向画“0”……
为啥中文的一二三笔画简单明了,零的笔画那么多啊?(中国〇的历史,这点其他回答仍然看到有误导以为0是源自印度,比如
理由居然是色即是空,且不说佛教和印度的关系,实际上真正现在使用的算术意义的0需基于十进位值制,占位符,负数三个基本概念才成熟,占位符可能容易出现,但另外两大因素目前文献和考古证据只有古代中国最先使用。流行的0源自印度按考古证据早就学界公认没有十进位值制,也没有负数的概念,即使产生什么虚空的0也和数学毫无关系。道听途说加个人臆断是妄史论的基本模式……而 也指出了其印度0的可能意义,更详细的0起源与传播史的学界考证可参考上答)
真正的数学史冷知识是欧洲对负数的接受相对中国晚的多(才发现
也提到了这点)17世纪,帕斯卡(B.pascal,1623-1662)对负数还持怀疑态度,并认为从0减去4纯粹是胡说。笛卡儿(R.Descartes,1596-1650)也只是部分地接受负数,并称方程的负根为假根,他的倾斜坐标系的x、y只取正值,图局限在第一象限之内。沃利斯( Wallis ,1616-1703)是一个例外,在1655年所著的《无穷大算术》中,他承认负数,但认为负数比无穷大大而不是小于0,并做了以下论证:由于比a/0在a为正数是为无穷大,所以当分母变为负数时,例如当a/b中的b是负数时,这个比一定比无穷大大。……
文艺复兴时期,西方对于负数有所了解,但对方程的负根都不承认和接受。16~17世纪的大多数数学家并不承认它们是数,或者即使承认了,也并不认为它们是方程的根。欧洲人在17~18世纪才逐渐承认负数……
——刘旻、齐晓东,《东西方对负数认知的历史比较》,《西安电子科技大学学报(社会科学版)》,2006年前04期
半枝莲:数理符号史 中 系列还提到更多数学传播史,如
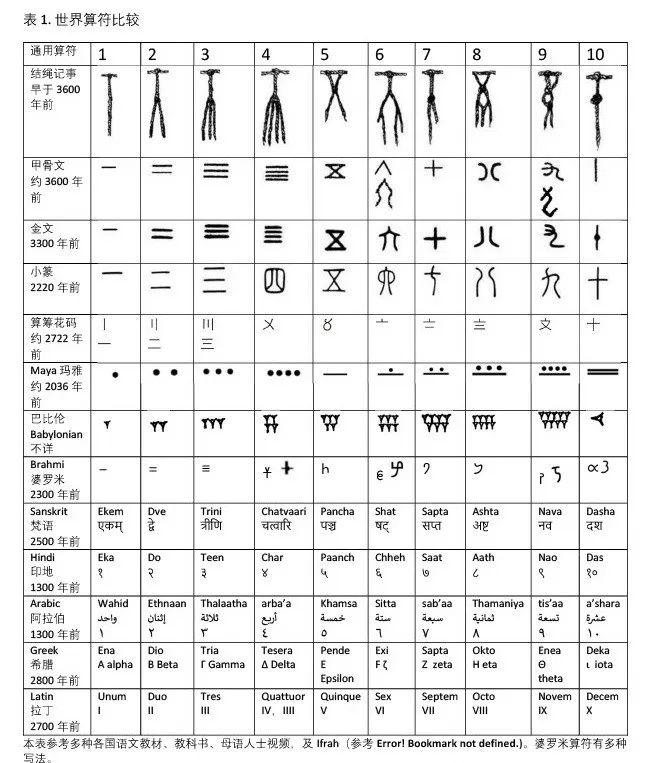
中国出土的战国算表(清华简),是世界上最早的。司马迁的“运筹帷幄,决胜千里”,用算筹计算兵力,路程,补给等等,说明算筹在汉朝已经普遍使用。汉张骞出使西域,开始了丝绸之路。可以想象这样一个场景:商人摆摊,在地上划价目,要快速完成交易,杂用花码、甲骨文、金文、小篆各种算符,连笔速写。买家在旁边或对面看,把符号侧写,倒写,演化成今天国际通用算符。
欧洲人称印度-阿拉伯数字自7世纪出现,由花剌子模(al-Khwarizmi,约西元780-850年)和肯迪(al-Kindi,西元796-863年)传入欧洲。7世纪正是唐朝丝绸之路活跃时期。7世纪以前,阿拉伯用什么算符呢?没有资料。最大可能是阿拉伯人改写中国的算符,传到欧洲。7世纪,欧洲人还没有直接接触中国人,只知道阿拉伯人有算符,误为阿拉伯人发明。
结绳、甲骨、金文、花码的I一,II二,III三,快写连笔成阿拉伯原型的对应数字,侧看是1,2,3。四的花码X 快写变成4 ,阿拉伯原算符的456不像通用算符。汉字”五”结绳到甲骨文一样,变异为花码快写〥,再变成通用算符5。6 的来源是结绳六的快写,把底部连起来成圈。结绳与甲骨文的七,演化为阿拉伯的V,倒看是“七”,保守的德国人写7字,中间加一横,是七字的倒写。甲骨文、金文“八”是结绳去掉中间支撑部分,本来八有分开的意思,通用算符8就是分成两个圈,结绳的形状也包含8,阿拉伯相应算符是把汉字的八上部连接。作为金文的快写连笔,爪变为拳,省去下弯,通用算符写作9。
阿拉伯,波斯,乌尔都(Urdu)的算符有许多共通处,但不是现代欧美的所谓“阿拉伯数字”(通用算符)。一般认为阿拉伯数目字是西元771年穆斯林王朝建立时,印度天文数学家Brahma Gupta 带来数学书(西元628年)出现算符,年代远远晚于中国的算符。
阿拉伯语言复杂的多音节与简单的算符不相称,没有算符之前,阿拉伯拼音文字如何计算值得深究。例如“二十三”,阿拉伯语发音是thalathah wa ishrun六个音节,跳绳要放慢速度才能数,要纪录复杂的算术,要大量音节。汉语“二十三”可以简化为“廿三”两个音节,速度快两倍到三倍。
中国算符从结绳到后来甲骨文,金文,算筹,珠算,民间码(花码),小篆,楷书,一脉相承。
在十进制中普的回答中也提到,十进位值制确实是中国原创并输出到世界,最後形成现代用的阿拉伯数系,印度阿拉伯据目前文献考证都只是中间商,学界已有公认论文专著论证(参考附录),只是类似结论还未更新入教科书和一些科普媒体。
十进制有什么优点?为什么世界各地的数学不约而同的选择了十进制?
另外可能对大众更冷的数学史知识是:无理数早在魏晋时期的刘徽已经有论述,如定义开方不尽数为面,并用类似近代极限逼近的算法讨论相关极限和误差问题,已经涉及到无限不循环小数(无理数)的构造算法。不过要强调下,这个无理数的概念是建立在中算范式上,与西数逻辑不同,不能按现代意义来理解,其差异可参考
中西传统数学是两种范式,基于各自背後的中西哲学差异,可参考
因此不能简单比较评价,以西数近代以后(基于工业革命与近代科学的推动)才有的成就来贬低中算其实是不合理的,更客观的比较应该基于16世纪前的中西数学史成就及对各自国家生产力的推动上。可参考吴文俊先生的数学史介绍或初步讨论
再看看西方历史:
20世纪20年代开始,才出现用"无限不循环小数"定义无理数。
历史上人们对无理数的认识,最早是从‘根号型’开始,后续陆续发现其他类型的无理数的存在,如:π、e等。而学生对无理数的认识与无理数的发展具有历史相似性,已有研究表明,虽然高中阶段和大学阶段会学习很多除‘根号型’和π以外的无理数,但学生最为熟悉的还是最初的这两种类型。现代教科书中均采用‘无限不循环小数’来定义无理数,这已完全脱离了无理数最初的起源,是‘深加工’的结果,学生对无理数的理解往往停留在表面,仅会从形式上判断是不是无理数,而不能从知识的本质上理解无理数的定义。而早期教科书无理数定义从不完善到完善的过程,为今日的教科书编写和课堂教学均带来启示。
(栗小妮、汪晓勤,《美国早期教科书中的无理数概念》,《数学教育学报》2017年06期)
对比中国数学史,
《九章》通过除法与减法运算而定义新型的数‘分数’和‘负数’,以及相应的各种运算规律,早已完成了‘有理数系统’。”(吴文俊,《中国古算与实数系统(一)》,《科学》2003年02期)
最迟明朝就有了类似导数计算的方法被王文素《算术宝典》记载下来(不代表有微积分),而牛顿莱布尼茨是清朝康熙时代的人物。
最後提下一些常见的数学史误区,都与毕达哥拉斯有关,一个是所谓的“毕达哥拉斯定理”并非来自毕达哥拉斯,至少目前文献考证除了很晚後人的转述传说,没有其证明过程的任何可靠记录,相反中国勾股定理被误认为只有特例的说法是错误的,早就被数学史学界纠正了,很多自媒体或教科书都没有更新,相关介绍参考
我国数学教材中的「勾股定理」是否应该改成「毕达哥拉斯定理(Pythagoras theorem)」?
另一方面,从中国古算文献序可初步了解中国文化中对数及算学的推崇,可以说“万物皆数”的思想其实是中国文化,而非只是所谓的古希腊毕达哥拉斯学派思想,後者不知是否有类似中国古算文献一样可靠的传世或出土文献记载流传下来,如仅仅是后人的转述,不妨看作一种西方传说,类似中国的后羿射日一类。中国算学文献相关记载暂列一些参考
《孙子算经》孫子曰:夫算者:天地之經緯,群生之元首,五常之本末,陰陽之父母,星辰之建號,三光之表裏,五行之準平,四時之終始,萬物之祖宗,六藝之綱紀。
南宋秦九韶《数书九章》序
周教六艺,数实成之。学士大夫,所从来尚矣。其用本太虚生一,而周流无穷,大则可以通神明,顺性命;小则可以经世务,类万物,讵容以浅近窥哉?……要其归,则数与道非二本也。
更多参考
开头提到的“妄史论”是一种极端伪史论,也是其他回答在批驳的民间自媒体宣传,主要是流量博眼球一类,要想真正了解全面的西方历史,可以参考正规的学界研究,一般称为“疑史论”,相关区分可参考

更多参考
古代中国数学,目前研究生的什么专业会研究它们?(中国数学体系的初步介绍,不只是很多人眼中的普通“算术”喔,这又是常见误区)
古代小孩也要学数学吗?(古代对数学教育的重视与普及)
中国古代数学书中为了研究有没有发明过什么特殊的符号用来做深层次的计算、证明或定理表示?
中国古代有没有产生科学的条件或潜质?(更多中国科学史介绍)
中文在数学表达上是否处于劣势?(中国数学的现代发展尝试)

附录:中印阿数学文化交流与数字比较
“我们可以断言,中国与印度文化交流的起点肯定在公元前3世纪秦统一中国以前,这恐怕是大多数人都能接受的意见。”
——《中印文化交流史话》薛克翘著,商务印书馆,1998年版,第8页

另外有知友观点是阿拉伯数字可能与中国数字漢字的草书简化相关,类似日本假名,可参考(比较印度与阿拉伯在现代阿拉伯数字前的数字及现在仍然阿拉伯部分地区实际用的数字,都和流行的阿拉伯数字形态部分差异较大,而漢字数字的草书简化或旋转如下图,确实更接近现代阿拉伯数字形态)

2世纪梵文字头数字(《数学符号史》/徐品方、张红著,科学出版社,2006年版,第62页):

瓜廖尔数系,876年(《学术史概论 第2版》/李文林著,高等教育出版社,2002年版,第107页)
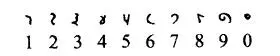
另外有相关考证可参考:
阿尔·花拉子米(约780出生于花剌子模~约850在巴格达市去世),花剌子模人。著名数学家、天文学家、地理学家,被西方誉为“代数之父”。作《算法》所言用“九个数码”表示任何数字,按现在学界研究应该来自中国算筹的十进位值制。
花拉子米出生地现为乌兹别克花拉子模州希瓦市,即昭武九姓的火寻国,位于今天的阿姆河下游、咸海南岸。至657年左右,昭武九姓诸国均已纳入唐朝的羁縻系统,隶属于安西大都护府或北庭都护府,是唐朝的直接管辖地。花拉子米出生时,唐朝已统治火寻一个半世纪。因此,按地域花拉子米及其祖辈都属于唐朝边民,花拉子米属于中国数学家。
再引网上关于蓝教授学术背景的介绍:
蓝丽蓉(1936-),新加坡著名的中国数学史学者,新加坡国立大学退休教授,国际科学史研究院院士。蓝丽蓉是新加坡企业家陈嘉庚的外孙女,李光前的姨甥女,原名温丽蓉,嫁与新加坡律师蓝秉湖后从夫姓。1957年,蓝丽蓉毕业于马来亚大学(今新加坡国立大学),后获得女皇奖学金赴英国剑桥大学深造。回新加坡后任新加坡大学讲师,1966年获新加坡大学博士学位。1988年晋升为新加坡大学正教授。她在新加坡大学数学系任教,前后长达35年,于1996年退休。
自1966年开始,蓝丽蓉在国际数学期刊发表关于《九章算术》、《杨辉算法》、《张邱建算经》等中算史经典的论文。从1974年至1990年兰丽蓉兼任国际数学史学会刊《Historia Mathematica》的副主编。
《数源》书中详述中国五世纪《孙子算经》的十进位制筹算的记数法则、和加、减、乘、除、分数运算、开平方运算的程序,还详细比较九至十世纪(原认为是)阿拉伯的著名数学家花拉子米、伊本·拉班关于印度算法的多种著作,发现阿拉伯国家早期关于印度算法中的四则运算和开平方方的程序,和孙子算经中的方法十足相同,从而提出印度-阿拉伯数字系统的十进位制概念,乃起源于中国算筹的学说。
蓝丽蓉的考证基于五点,其思路非常明确:其一,阿拉伯数字出现以前,最早出现十进制的国家是中国;其二,阿拉伯和印度古代的所有典籍记载中全无十进制的影子;其三,中国在三世纪以后,和印度、阿拉伯世界一直有多路的文化商业交往;其四,中国算筹曾传播到日本、韩国等地,且这些国家史籍皆有记载;其五,中国的筹数运算法则和现代阿拉伯数字的相应法则基本同构。以上五点在《雪泥鸿爪溯数源》中得到了充分的论证。
该书于2004年再版,内容大致和92年版相同,但增加一篇她在2002年在北京召开的国际数学史大会上,在荣获凯尼斯·梅奖之后的致谢演讲,题为《中国古代的数学及其对世界数学的影响》。
