总结:至多错了个5分的选择和5分的大题,这把至少110分
问题1
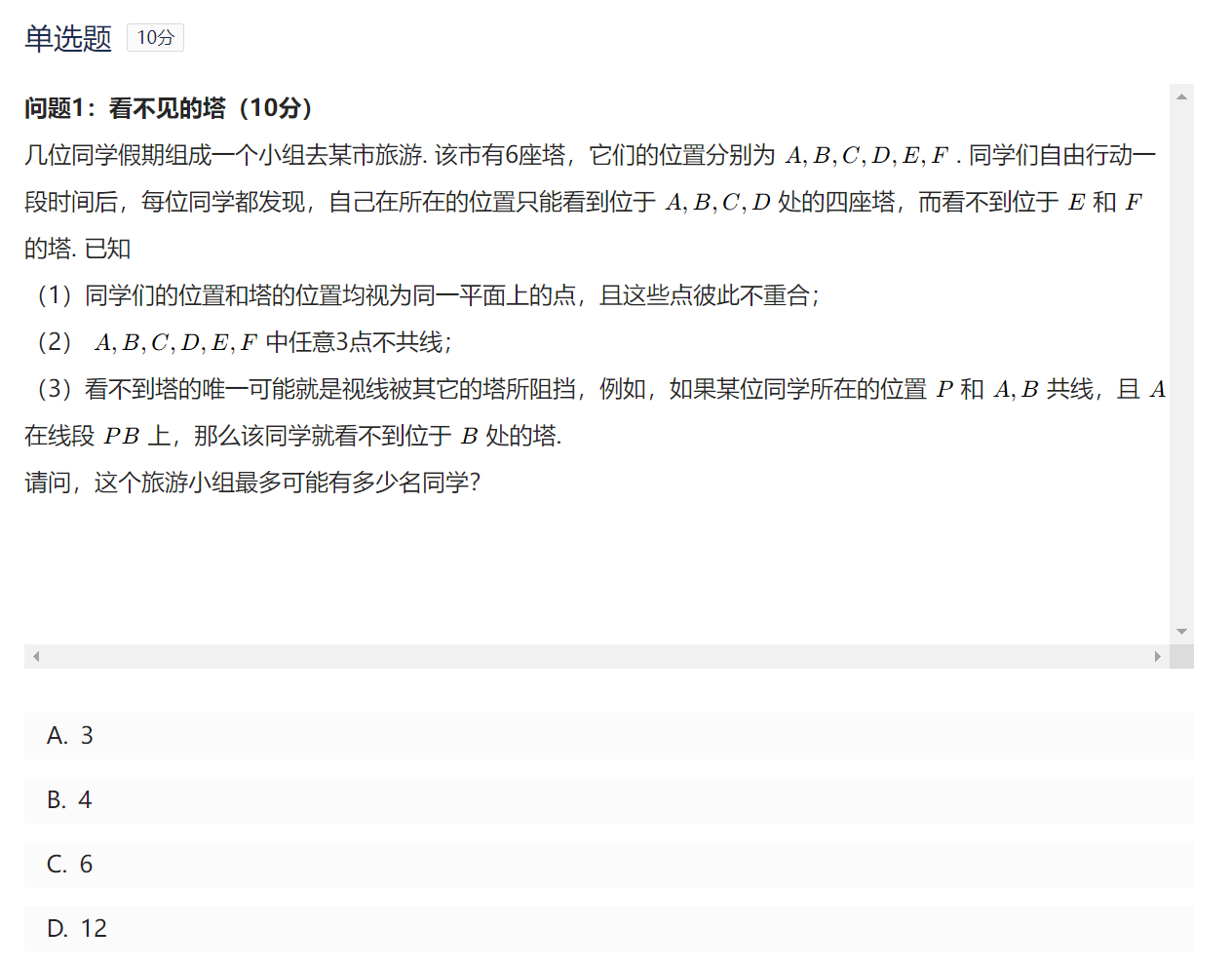
Proof.答案至多是组合数 {4\choose 2} ,又因为可以构造出最大的情况,所以是6,选C.
问题2(1)
直接写程序
import numpy as np
# 初始参数设定
initial_score = 2.0
score_gain = 1.5
hit_probability_decay = 0.85
# 计算小明在不同决策点的期望积分
def expected_score_after_n_fights(n):
# 初始积分和击落积分增加
score = initial_score
time_cost = 0 # 时间代价计算
for i in range(1, n + 1):
hit_probability = hit_probability_decay ** i
score += score_gain * hit_probability # 击落敌机获得积分的期望贡献
time_cost += 1 # 每架敌机的出现时间期望为1
# 如果小明被击落,游戏结束,期望积分即为当前计算的积分
if np.random.random() < (1 - hit_probability):
break
# 时间代价,每单位时间积分减1
final_score = score - time_cost
return final_score
# 模拟多次以获取平均期望值
def simulate(n, trials=10000):
scores = [expected_score_after_n_fights(n) for _ in range(trials)]
return np.mean(scores)
# 测试 1, 2, 3, 4 架敌机后的情况
n_options = [1, 2, 3, 4]
results = {n: simulate(n) for n in n_options}
results根据模拟结果,小明在击落第2架敌机后退出游戏可以期望获得最大的积分,其数学期望大约为2.35分。因此,为了最大化游戏结束时的累积积分,小明应该选择在击落第二架敌机后主动结束游戏。所以正确答案是选项 B.2
问题2(2)
这题没太懂题目,继续写程序
import math
def simulate_game_fixed_intervals():
score = 2.0
time = 0.0
enemy_count = 0
scores = []
while score > 0:
# Fixed time to next enemy: e^(-n), where n is the enemy_count + 1
time_to_next_enemy = math.exp(-(enemy_count + 1))
time += time_to_next_enemy
# Score decreases linearly with time
score -= time_to_next_enemy
# Check if score drops to zero or below
if score <= 0:
score = 0
break
# Increment enemy counter
enemy_count += 1
# Probability of defeating the enemy
p_defeat = 0.85 ** enemy_count
# Decide if defeated or defeated by the enemy
if np.random.rand() <= p_defeat:
# Defeated enemy, score increases
score += 1.5
# Record score if choosing to exit
scores.append(score)
else:
# Defeated by enemy, game ends
score = 0
break
return scores
# Simulate the game many times to find optimal stopping scores with fixed intervals
def find_optimal_score_fixed_intervals(num_simulations=10000):
all_scores = []
for _ in range(num_simulations):
scores_in_game = simulate_game_fixed_intervals()
all_scores.extend(scores_in_game)
# Compute the mean score for each possible exit point
if all_scores:
average_score = np.mean(all_scores)
else:
average_score = 0
return average_score
# Run the simulations with fixed intervals
optimal_score_fixed_intervals = find_optimal_score_fixed_intervals()
optimal_score_fixed_intervals跑出来是6,所以猜了个C.
问题3

这题第二问的第二种情况做了17h也没做出来啊啊啊啊......
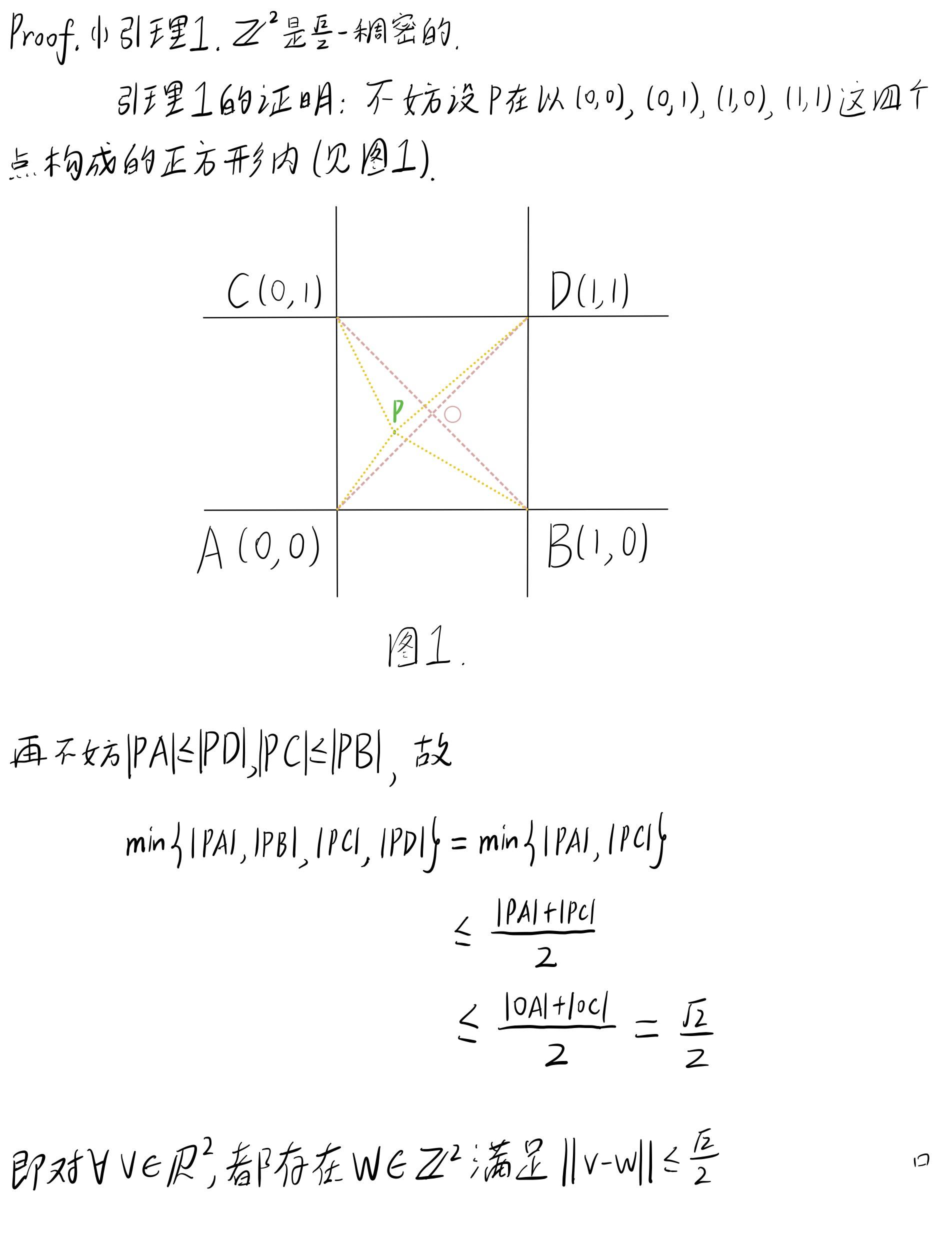




问题4

高等代数竞赛题






问题5

这题背景肯定是Löwner-John ellipsoid,但是原定理的结论没法解决原题,最多只能把系数做到9而不是3,所以还需要再结合题目里的中心对称性改进定理证明:






问题6




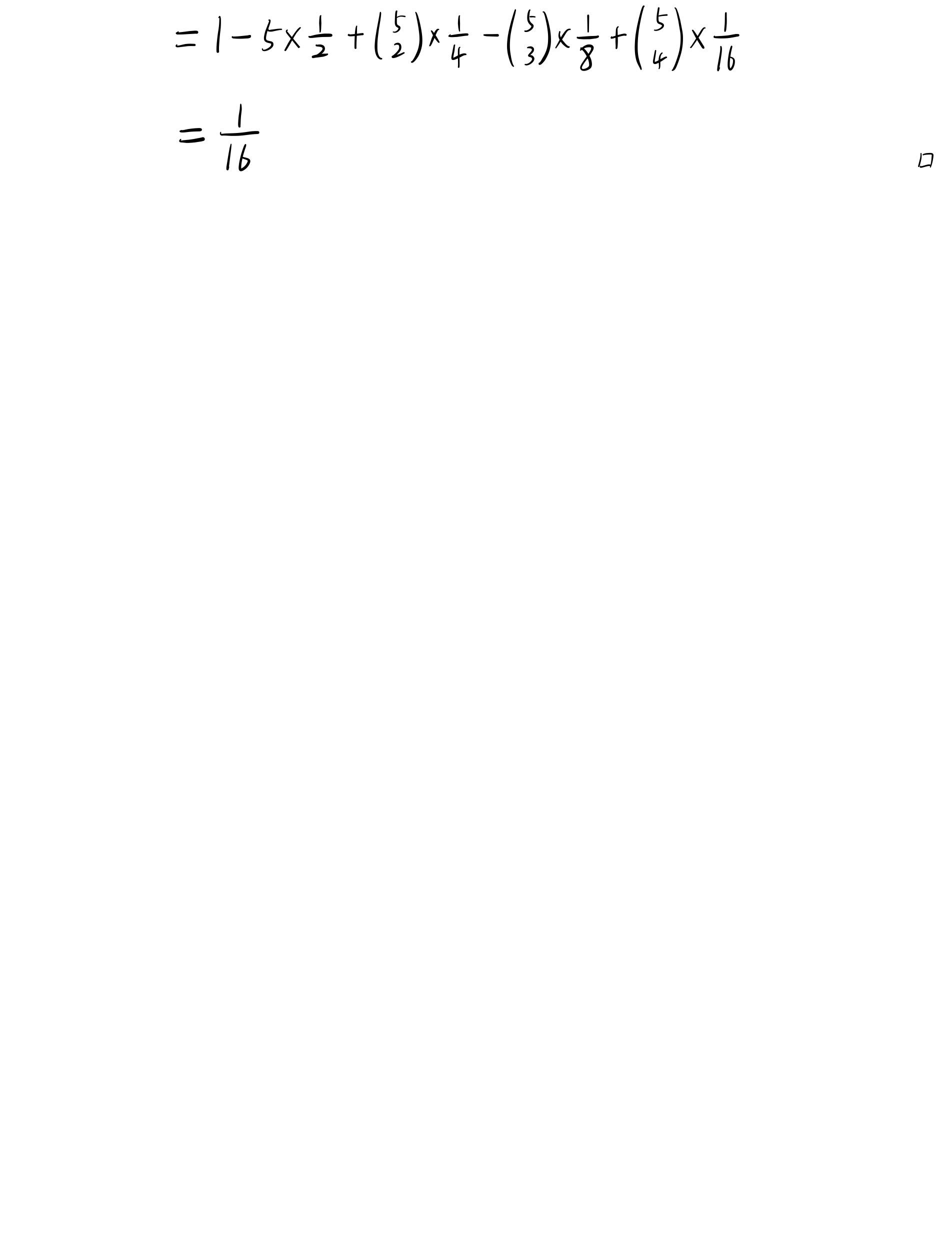
问题7







编辑于 2024-04-16 23:03・IP 属地陕西