《用AI嘎嘎乱杀国际数学大赛,是一种怎样的体验?》
数学,不存在了。
别笑,这就是我用AI做完阿里数学竞赛全部7道题后的第一反应。
昨天,我参加了阿里举办的全球数学竞赛,这也是我第一次参加正式的数学竞赛。
竞赛采取线上形式,任何感兴趣的人都可以注册参与。参赛者需要在2天内解决7道题。这些题目由评委新出,难度较高,虽然不及IMO那样变态,但远超一般的高考或大学高等数学的水平。表面上是开卷,其实题目的难度令人望而生畏。
我的身份比较特殊——我代表AI参赛。我的任务是让AI解决这些问题,而非亲自动手。坦白说,这些题绝大部分我都做不出,有些甚至连题目都看不懂。虽然我多年前学过理论物理,好歹攒了点数学基础,但毕竟不是数学专业出身,也缺乏竞赛经验,在学霸云集的赛场如同炮灰。不过,用AI参赛就完全不同了。我会不会做题不重要,AI会做题才重要。
其实,一开始我怀疑所谓的“AI赛道”只是一个噱头。
如果AI真能达到秒杀国际数学大赛的水平,那为什么我没听说过哪个科学家因为被AI取代而上天台?
如果不能——那我岂不真成炮灰了?
然而,真实情况远比我想象的更加惊心动魄。
我交卷后的总体感觉是,只要找到正确的方法,掌握操控AI的技巧,AI解题就是嘎嘎乱杀。有些题目我甚至还没看完,就丢给AI去解,我只需将结果复制粘贴上去,整个过程不到几分钟。
但这就引出了一个问题:
这是否意味着AI的解题能力已经超过了人类?
其实,现实远比想象复杂。谈到AI的数学能力时,我们往往会泛泛而谈。但通过这次比赛的实操,我对AI的数学水平有了切身体会。我认为,AI在数学方面的优点和缺点同样明显。
我将AI解题的方法分为三类:
第一类是数值模拟题。
这类题目不一定需要逻辑推导,可以通过编程方法进行数值模拟。例如,概率题通常可以通过模拟实验来求解。
为了方便大家(特指不懂数学的人)理解,我先举个低幼的例子。比如抛硬币,只要这个硬币两边对称,当你抛的次数 n趋向于无穷大时,两面出现的概率分别是多少?
如果把这个问题看作一个物理实验,真的找一枚硬币抛一万次,记下的次数差不多就是50:50。
在物理世界中真的抛一万次硬币还是比较费事的。但如果用计算机的随机数发生器模拟抛硬币的过程,所谓抛一万次硬币,也就是一段简单的python代码运行一万次而已,都用不了半秒。
比如,这次比赛中有一道“打飞机”题目。不要误会,是在游戏里打飞机:用你的飞机把敌机击落,得1.5分;如果被对方击落,game over。每过一关,后面的游戏越来越难,敌机把你击落的概率大增。游戏有个扣分机制,你玩游戏的时间越长,扣分越多。所以为了使游戏结束时的积分最大化,你的最佳策略是见好就收:一旦连续击落n架敌机,就主动结束游戏。
问题是,这个n是多少?
我要求GPT4给我用于数值模拟的python代码。不到10秒,GPT就写完了代码,只有40行:
def simulate_game(exit_after):
score = 2 # 初始积分
time = 0 # 游戏时间
n = 0 # 击落敌机数
while True:
# 计算下一架敌机出现的时间
time_to_next_enemy = np.random.exponential(1)
time += time_to_next_enemy
score -= time_to_next_enemy # 积分随时间减少
if score <= 0:
# 积分耗尽,游戏结束
return score
n += 1
# 小明击落敌机的概率
success_probability = 0.85 ** n
if np.random.rand() < success_probability:
# 击落敌机,积分增加
score += 1.5
if n == exit_after:
return score
else:
# 被敌机击落,游戏结束
return score
def estimate_expected_score(exit_after, num_simulations=1000000):
scores = [simulate_game(exit_after) for _ in range(num_simulations)]
return np.mean(scores)
# 测试不同的退出策略
options = [1, 2, 3, 4]
results = {option: estimate_expected_score(option) for option in options}
print("Expected scores for different strategies:")
for option, result in results.items():
print(f"Exit after {option} enemies: Expected Score = {result:.4f}")
对于题目的每个选项,各模拟运行100万次,求平均积分。程序输出结果为:
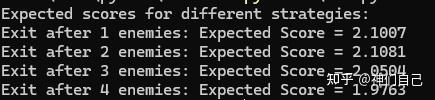
显然,n=2时退出,积分最高。
如果每一道题都是概率选择题,AI肯定100分,因为根本不可能错——假如模拟掷100万次骰子的结果是错的,那数学真的不存在了!
但比赛中还有第二类题型:逻辑推理题。
典型如证明题,结果是已知的,要的是过程。AI必须给出每一步的推理,只要错一步,整个证明就不成立。
没想到,强如GPT4,也在这类题上碰了钉子。
出人意料的是,GPT4能够给出完整的分析思路,却打死也不愿意把题做完。
比如第4题,要求证明f的全部特征值为-d,-d+1,……,d。
以下是GPT的回答,我省略了一些细节:
为了证明线性变换 \( f \) 的全部特征值为 \( -d, -d+1, \ldots, d \),我们首先需要更深入地分析变换 \( f \) 的定义和其作用。
步骤 1: 理解 \( f \) 的作用
步骤 2: 建立 \( f \) 的矩阵表示
步骤 3: 分析 \( f \) 的特征值
步骤 4: 特征多项式和对称性
步骤 5: 考虑特殊情形和归纳法
由于问题的复杂性和特定性,完整的解析解可能需要高级的数学工具(如矩阵理论、特征多项式理论、可能的群论或对称性分析)。
我强烈怀疑GPT4的训练数据有缺陷。OpenAI在数学领域的训练语料可能缺乏具体的推导细节,导致GPT4推理时只能给出大纲式的解题思路,每一条都正确,每一条都没什么卵用。
多次调教GPT无果后,我转向了Claude3。
Claude3出了之后,有人说它比GPT4还强,也有人说感觉差不多。
然而在数学的形式逻辑推理领域,我发现,Claude3有了巨大的进步,进步之大连营销号都吹不出来。
以下是Claude3对第4题第1小问的证明,无任何删节,一字不改:
我们将分步骤进行证明。
步骤1:证明U_j是f的不变子空间,且f在U_j上的特征值是-d+2j。
对于任意向量v∈U_j,可以写成v=∑_{k=j}^{d-j}a_k v_(2k+1),其中a_k是一些复数。那么
f(v) = f(∑_{k=j}^{d-j}a_k v_(2k+1))
= ∑_{k=j}^{d-j}a_k f(v_(2k+1))
= ∑_{k=j}^{d-j}a_k ((2k)(2d-2k+2)/2*v_(2k) + 1/2v_(2k+2))
= ∑_{k=j}^{d-j}a_k (k(2d+1-2k)v_(2k) + v_(2k+2))
= ∑_{k=j}^{d-j-1}(a_k+a_(k+1)(k+1)(2d-2k-1))v_(2k+2) + a_j j(2d+1-2j)v_(2j+1) + a_(d-j)(d-j)(2j+1)v_(2d-2j+1)
观察上式,f(v)的表达式中只包含v_(2j+1),v_(2j+3),…,v_(2d-2j+1),所以f(v)∈U_j。因此,U_j是f的不变子空间。
再看系数a_j j(2d+1-2j)和a_(d-j)(d-j)(2j+1),它们分别是v_(2j+1)和v_(2d-2j+1)的系数。注意到
a_j j(2d+1-2j) = a_j(d-(d-j))(2d+1-2j) = a_j(d(2d+1-2j)-d^2+dj)
= a_j(2d^2+d-2dj-2d^2+2dj) = a_j(-d+2j)
a_(d-j)(d-j)(2j+1) = a_(d-j)((d-j)(2j+1))
= a_(d-j)(2dj-2j^2+d-j) = a_(d-j)(d(2j+1)-2j^2-j)
= a_(d-j)(2dj+d-2j^2-j) = a_(d-j)(-d+2j)
所以,在U_j的基v_(2j+1),v_(2j+3),…,v_(2d-2j+1)下,f的矩阵表示中对角线元素都是-d+2j,其余为0。因此,-d+2j是f在U_j上的特征值。
步骤2:V是U_0,U_1,…,U_⌊d/2⌋的直和。
首先,U_j(0≤j≤⌊d/2⌋)的维数之和等于V的维数:
∑_{j=0}^{⌊d/2⌋} dim U_j = ∑_{j=0}^{⌊d/2⌋}(d-2j+1) = (⌊d/2⌋+1)(d+1)-2*∑_{j=0}^{⌊d/2⌋}j=(⌊d/2⌋+1)(d+1)-⌊d/2⌋(⌊d/2⌋+1)=2d+1
其次,任意两个不同的U_j和U_k(0≤j<k≤⌊d/2⌋)的基是不相交的。因为U_j的基向量的下标是2j+1,2j+3,…,2d-2j+1,而U_k的基向量的下标是2k+1,2k+3,…,2d-2k+1,两组下标没有交集。
因此,V是U_0,U_1,…,U_⌊d/2⌋的直和。
步骤3:f的特征值为-d,-d+2,…,d-2,d。
根据步骤1,f在每个U_j(0≤j≤⌊d/2⌋)上的特征值是-d+2j。
当j从0取到⌊d/2⌋时,-d+2j的值就是-d,-d+2,…,d-2,d(当d为偶数)或-d,-d+2,…,d-1(当d为奇数)。
再根据步骤2,V是U_0,U_1,…,U_⌊d/2⌋的直和,所以f在V上的特征值就是它在所有U_j上的特征值的并集,也就是-d,-d+2,…,d-2,d。
综上所述,我们证明了f的全部特征值为-d,-d+1,…,d-1,d。证毕。
虽然做题的不是我,但是当AI一气呵成地吐出答案时,我突然产生了一种不可名状的爽感。
结尾潇洒的“证毕”二字,更是让我梦回当年在满黑板的公式最后,狠狠写下“Q.E.D”、然后扬长而去的峥嵘岁月。
而现在,即使让我返老还童,我也不愿去学数学了。
没关系的,都一样。
这才是Claude3真正超越GPT4的地方。也许Claude团队真的搞到了一批专业数据,也许部分数据是用强化学习生成的——总之,他们必定在数据上下了大功夫,否则无法解释证明过程怎么会写得如此详细。
我还听说过一个案例:有人把显微镜下的医学病理图片发给Claude3,结果它不仅能识别出这是什么标本,甚至能指出这个标本里的哪些特征很可能代表某些病变!
不过我敢说,即使GPT4+Claude3双管齐下,仍然不可能拿满分。
因为两大AI唯一做不出的题,恰恰是本次比赛最简单的题。
这就是我总结的第三类题型:平面几何。
我来用不严谨的科普语言给大家说说第一题:
有6座塔和n个人,塔和人都用一个点表示。当塔和人恰好处在某个位置上时,会产生一个奇特的效果:所有人都能看见4座塔,但所有人都看不见剩下的2座塔,因为所有人望向那2座塔的视线都被其它塔挡住。请问:n最多是几个人,才能保持这种奇特的效果?
就是这道题,让两个AI左右为难。
一开始,GPT和Claude都以为n的上限是无穷大,也就是无论多少人,视线都能被挡住。
这种情况是有可能的,比如所有塔和所有人都在一条直线上。但这恰恰是题设明文排除的,因为题目规定塔不能3点共线,所以两座隐藏的塔不可能被一条视线同时穿过。
当我给AI解释明白之后,它们又开始怀疑,是不是2个塔被围在4个塔内部,所以看不见。我苦口婆心地告诉它们,塔是一个点,围起来也挡不住。但GPT似乎倔强地认为,塔不可能是一个点,而是一个巨大的圆柱体……
最后,无可奈何的我只得祭出数值模拟大法。我要求AI生成一段python代码,画出人和塔的所有位置。人用P1、P2、P3表示,塔用A-F表示。如果人的视线能看到塔,画红线;看不到,画绿线。
经过几次尝试后,GPT4终于给出了正确的代码,画出的图形如下:
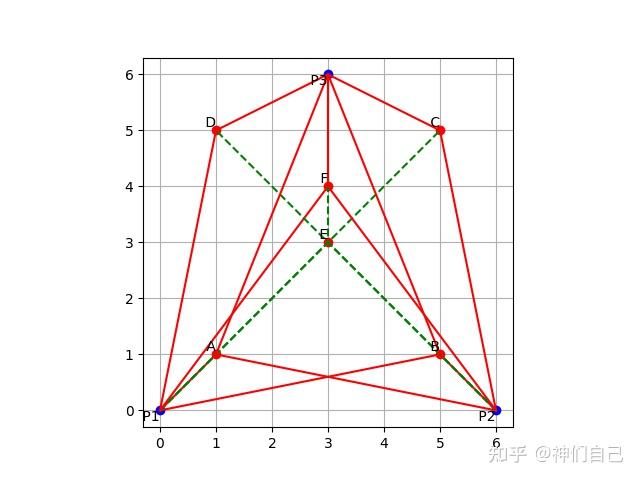
这显然不符合题设。图中只有塔E被隐藏,另一座塔F所有人都能看到。
当我把图片传给GPT后,它爽快承认了错误,并按我的要求重新调整了塔和人的位置布局。
然后生成的图片错得越发离谱……
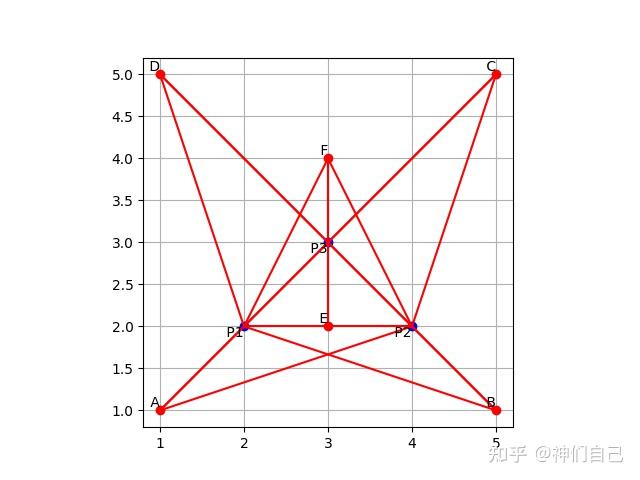
难道这题真的这么难?
凭借多年的做题家经验,我可以肯定地说,不可能。
做题不是打打杀杀,做题是人情世故。
第一题,是评委老师和你交个朋友的,就算不是最简单,也绝不可能难到下不了口。
我在草稿纸上画了几笔,突然发现了一条思路:
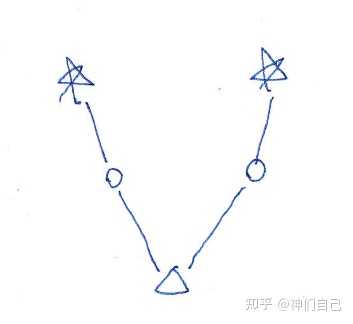
五角星表示隐藏塔(看不见),圆圈表示普通塔(看得见),三角表示人,直线代表视线。
假设只有1个人,2座隐藏塔要想不被这个人看见,唯一的方法是有2座普通塔来遮挡视线。
既然挡住1个人需要2座普通塔,那么挡住3个人就需要6座普通塔。
但题目中总共只有4座普通塔!这就意味着,必然有一些塔,能同时挡住2条视线。
顺着这个思路画下去,就是:
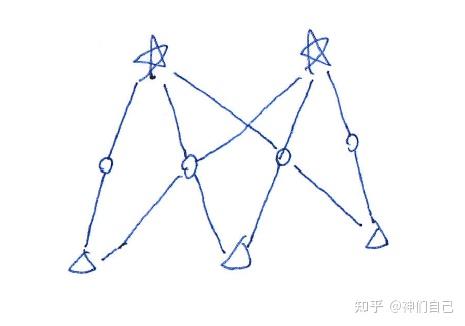
题目似乎已经解出:3个人如此排布,可以恰好让所有人都看到4座塔、看不到2座塔。
但多年的做题家经验在隐隐警告我:事情真有这么简单?
做题不是请客吃饭,做题是一群人淘汰另一群人的智力运动。
老师愿意让所有人做出,不代表老师愿意让所有人做对。
我突然发现,我漏掉了一种情况:一座塔可以同时遮挡2个人的视线,只要这两人在一条直线上。
所以,第4个人可以出现在一个妖孽的位置——别人的身后:
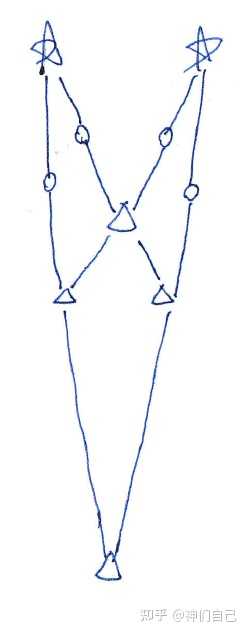
还没完。再仔细观察,发现有2座塔如果挪一下位置,还可以塞2个人进去:
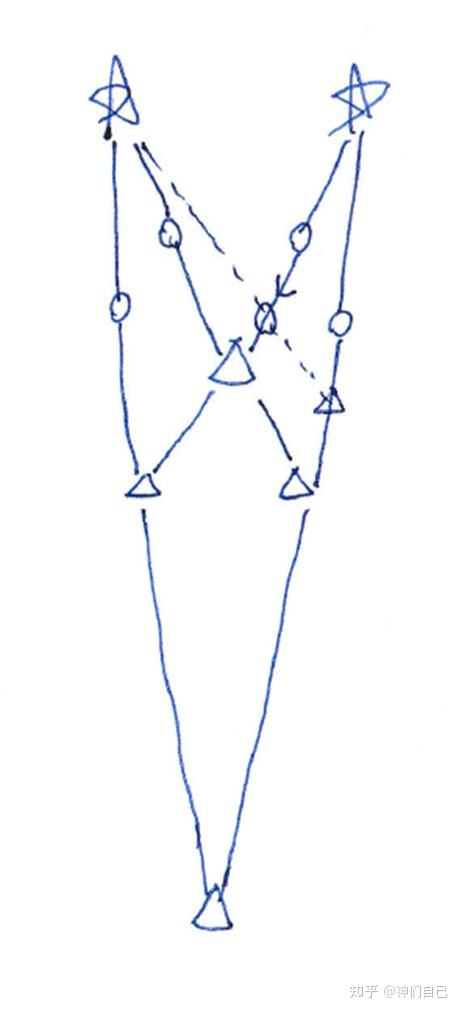
我把我的思路告诉AI,它们却仍然做不出。也许就是大语言模型AI的弱点:它们没有真正意义上的空间想象能力!这也难怪,尽管AI具有一定的图像识别能力,但它的思维逻辑仍然基于字符token,难以进行空间想象。而人类却是纯粹的视觉动物,我们看到的文字,其实只是视网膜上的一串光点。当我在草稿纸上画图时,AI脑子里的草稿纸又在哪里呢?
不过,我听说DeepMind最近发表的一篇论文找到了新方向,30道IMO平面几何题AI能做对25道,IMO金牌选手的平均水平也只有25.9道。而这样强大的AI,居然只有1.5亿参数!
其实,早在没有AI的70年代,就有计算机证明平面几何的成功案例了。它的原理是:把几何图形转化为一系列约束条件,比如三角形中两个角相等,然后写成规范的符号形式。因为欧式几何的公设和定理都极为有限,所以把这些定理都试一遍,就能得到一批推导后的等式。
比如,三角形中两个角相等,可以推出两个边也相等。把这些推导出来的等式加入题设,然后不断迭代,直到推不出新的等式为止——那么所有推出的等式,就是这道题所有可能的答案!而出题者要你证明的等式,也必然在其中!
这个方法在上世纪70年代,由吴文俊院士提出,史称“吴方法”。然而,虽然穷举法表面上无敌,真做起题来,IMO 30道只做对5道。原因在于,很多几何难题是需要画辅助线的,而且往往不止一条!画辅助线是一种艺术,简单的穷举式推理做不到——这正是DeepMind用AI模型解决的问题。他们把几百万道几何题及其答案转为符号逻辑形式,输入模型训练,让AI学会画辅助线,从而“吴方法”获得新生。
时间关系,这个新模型我就没空实验了。不过,如果沿着这条路走下去,让AI学会用符号逻辑的方式推理几何题,恐怕也不是难以企及的幻想吧?
我突然想到一个问题:有没有一种可能,这是第一届AI数学竞赛,也是最后一届AI数学竞赛?
如果AI的短板被迅速补上,长板继续加强,会不会超过人类?会不会——
会让一些长期未解的数学问题得到解决,如哥德尔不完备定理中提出的问题,或是各种猜想如黎曼猜想等。这将是数学领域的巨大突破;
会帮助人类发展新的数学理论和模型,推动数学本身的边界;
AI和人类数学家可以形成合作关系,各自发挥优势,共同推动数学和相关领域的发展,激发人类在数学和其他科学领域中的创造性思考。
总之,AI的发展稳中向好,对人类文明有巨大的帮助,我是长期看好的!
——GPT4如是说。