这次的初赛终于出了一些有点意思的题目,翻到最后可以看到我自己的答案。另外,我这个喵写数学证明的风格比较随手,和很多大佬不一样,我喜欢在写证明的时候保留脚手架,以便让人即便不看我的过程细节也能知道我在干什么。
总的来说,我认为这次的题目还是有一定难度,虽然很多问题本身叙述很高等,但是很多仍然可以通过巧妙的观察较为初等地解决。
另外,我很期待AI的表现。大胆预测一下AI能做对一个或两个选择(毕竟看起来比较好猜答案),然后大题就不好说了,要看它的知识库是否包含例如李代数表示具体的计算以及John椭圆的技巧,尤其是这里的中心对称情形(第四第五两题,不知道是否有文章具有直接的结论,如果没有的话AI仍然很难攻破。第三题的线性代数技巧太细,目前的transformer在数学问题上,很难给出完整严谨的证明,即便通过对语言模型做比较好的fine tune以及引导)。不过第六题应该是AI有希望做出来的。最后第七题AI可能难以写出对应距离的动力系统和映射,可能难以进行。
首先我们来简单观察一下每题都考察什么。
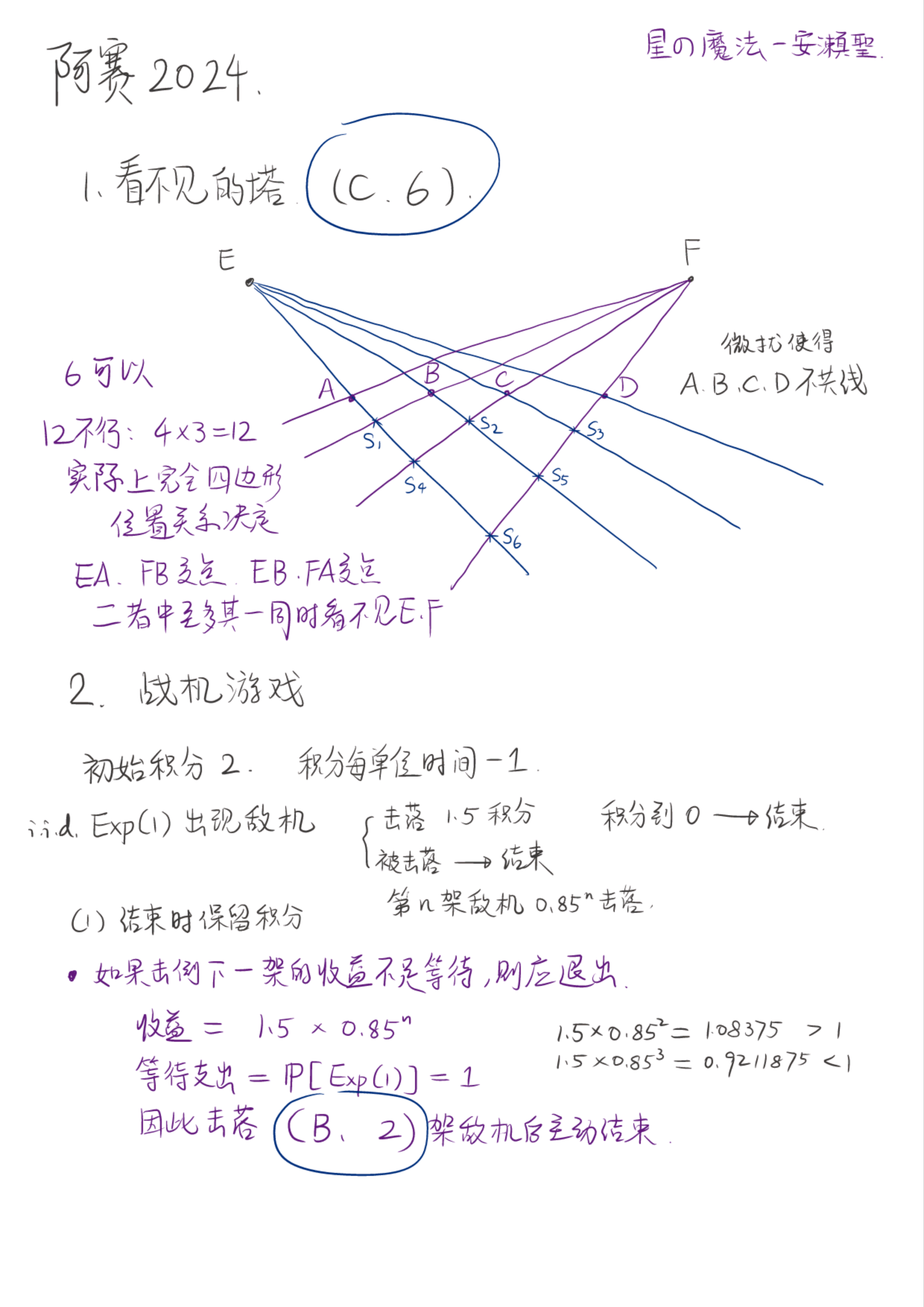
☆第一题,看不见的塔,考察组合几何,通过分析完全四边形和直线上的序得到证明,例如对塔EF和AB,那么连线EA和FB交点以及EB和FA交点,二者至多其一是符合条件的,所以一下就能证出来是12/2=6。这个题目是这一类凸性分析的组合几何问题中最“轻量级”的,比较适合作为选择题。
☆第二题,战机游戏,这个题考察的是连续时间的概率论和博弈论,尽管如果要严格地证明什么策略最优是数学上很困难的,但是通过某些“博弈常识”可以将问题变成例如函数和数列的最值。
其中第一小问可以完全离散地计算等待下一架敌机的得分期望。第二小问则较为困难,经过计算会发现这样一些“直觉”,例如:如果已经等了一会,敌机还没来,那么你应该一直等,否则早在当初“决定去等”的时候就要主动退出了。这不只是因为等的时间分数掉了是沉没成本,而且分数越少越应该“放手一搏”。
最后第二问的最优策略理应是,无论如何都等第一架敌机,打完后就跑,绝不等第二架,这样算出来准确概率是 \frac{17}8-\frac{17}{4e^2}\approx 2.07 。这也和上面的分析相符,最优策略一定是“很决绝”的。
☆第三题,线性映射作用在平面格点的【稠密性】。这个题两问可以有不同的看法。在一开始考虑的时候,很自然地使用特征值来计算,但是这不够优美!聪明的办法是,注意第一问迹0的2阶矩阵,平方一定是数量矩阵,这意味着像格点的“形状”只有两种。第二问我们只需要用Minkowski找一个很短的像格点,然后A作用上去就能得到一个线性无关的格点(数论在这里发挥了作用),这时候二者生成了一个基本平行四边形(在椭圆曲线等理论中,大家也管它叫fundamental domain),这个平行四边形两条边长度都很短,所以它本身也很小。
实际上第三题之所以能这么做,我们观察失败的例子会更直观,例如为什么对角线上放1,2的矩阵(特征多项式是 (x-1)(x-2) 可约)为什么不行呢?因为它的幂次下1那一侧没有增长,导致它的四边形在一个方向被无限拉长,而如果它是一个二次数域的子格(甚至是order),那么你可以用复乘一个代数整数真的造出basis。
☆第四题,一个看起来是线性代数具体计算的李代数表示论。这个题有两种攻克途径,对于数学物理学家来说,暴力计算找规律绝对是重要的研究手段,所以我一上来就写了一个mathematica代码来计算。但是同时,在看到题的一瞬间,这些系数应该使你隐隐约约感受到sl2表示的味道。于是计算的辅助下,你发现换元vi乘某个阶乘竟然能将它们直接对应sl2的2d+1维的齐次多项式表示!
X=\left[\begin{matrix}0&1\\0&0\end{matrix}\right],\ Y=\left[\begin{matrix}0&0\\1&0\end{matrix}\right],\ H=\left[\begin{matrix}1&0\\0&-1\end{matrix}\right].
那么这时候你就只需要“构造字典”,就是把题目中的语言完全转化为sl2表示里的语言,首先是它的f,对应sl2表示的 (X+Y)/2 ,所以是半单元,它的特征值是标准的 H 的一半,一个小技巧是注意到半单李代数的Cartan子代数都是共轭的,所以其中的半单元可以通过内自同构变过去,所以特征值就是一半,而 2d+1 维表示的标准H特征值我们熟知是 -2d,-2d+2,\cdots,2d ,所以这里的f就具有一半的 -d,-d+1,\cdots,d 就是如同题目要求那样的特征值。这个内自同构甚至是一个对合,相当于李群SL2中元素 \frac1{\sqrt 2}\left[\begin{matrix}1&1\\-1&1\end{matrix}\right] 的共轭作用,可以具体写出来,它就是
X\mapsto \frac12(H-X+Y),\ Y\mapsto \frac12(H+X-Y),\ H\mapsto X+Y.
剩下两个小问就是具体去算,然后找更多的规律了…我不知道有没有更多表示论背景,反正我是硬来的,知道背景的小可爱可以说一声。
☆第五题,本题是真正的组合几何与凸优化。首先要知道小学二年级就学过的,John 椭球的背景知识,不知道的小可爱们可以上wiki什么的搜一下。大概就是说,对于欧氏空间的一个有界凸集,存在唯一最小体积的外接椭球(这个椭球其实把凸集包裹得很好,很容易猜测它就是符合条件的解),但是有的小伙伴会说,不对啊,题目要求的是面积最小啊?这里就是这个问题特有的技术细节了。
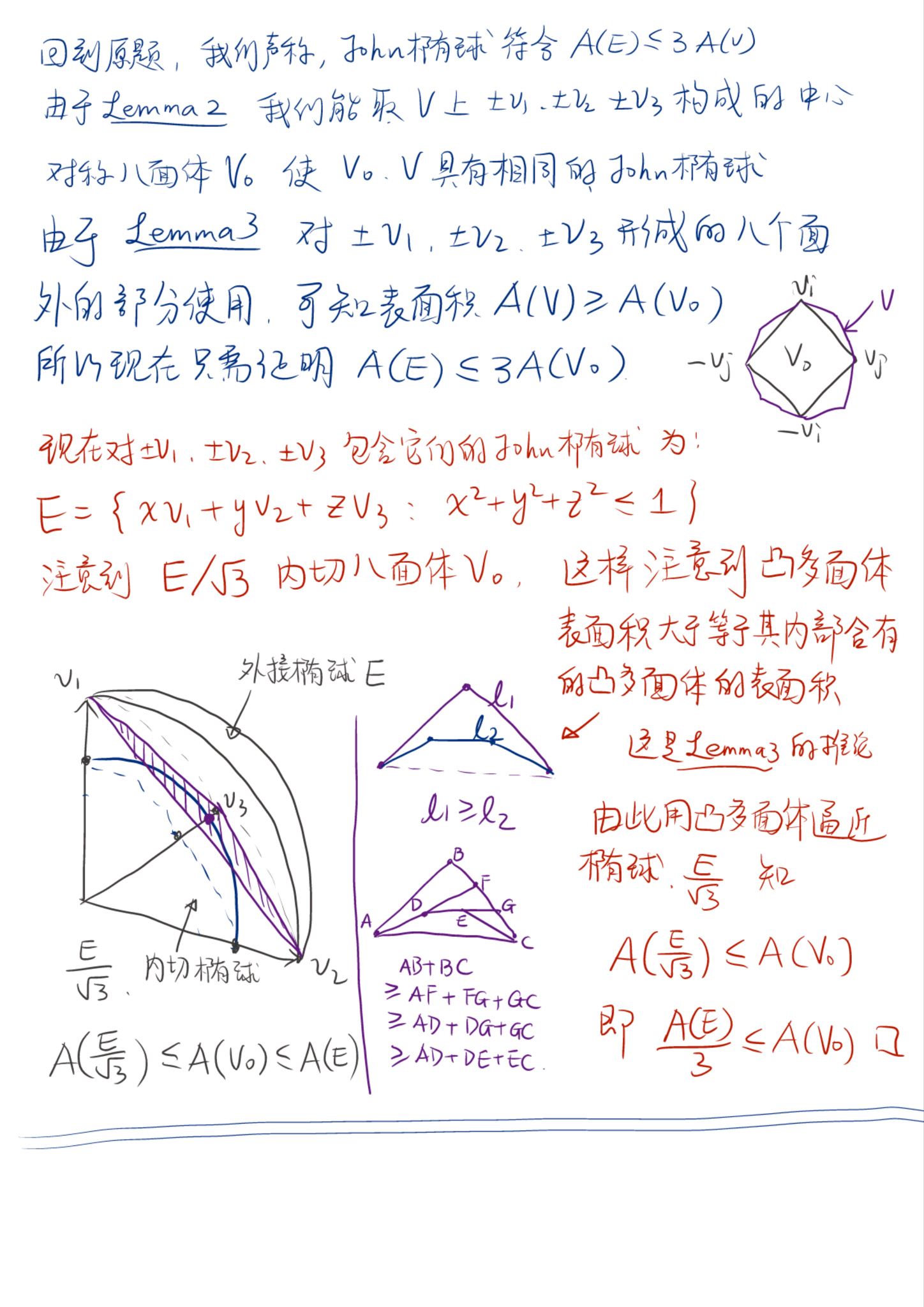
对于中心对称的凸集 V ,利用John椭球的唯一性,我们其实可以证明出来John椭球 E 也得是中心对称的,然后接下来的技巧大概就是证明这个椭球的 1/\sqrt 3 倍实则内含(可以有切点)于凸集 V ,以及三角不等式的高维推广,得到包含的凸集其表面积也具有不等式关系。所以
A(E)\ge A(V)\ge A(E/\sqrt 3)=A(E)/3.
这里 A 表示表面积。实际上通过一些观察把问题化归为中心对称凸八面体的情况,可以证明 3 可以被换成更优的常数 \pi/\sqrt 3 ,这也是正八面体时的比值 A(外接球)/A(正八面体) 。
☆第六题,本题的背景是生成函数/Fourier变换/有限状态Markov过程。相比前面的问题来说,这个问题绝对是最友好的一道题,简单来说,我们应该指望最后的奇偶性应该是充分均匀的,在样本数很大的时候我们应该不大能得到什么奇偶信息。
那么证明这种结论的技巧有几种,首先最容易想的办法就是直接算,实际上因为是独立的Bernoulli分布,它的生成函数是极其容易求出来的,在此之后,计算奇偶无非就是代入 \pm1 然后取平均,一个硬币是取 1/2 的平均,本质上说一个硬币其实可以看作两个福,一个【正面福】和一个【反面福】。而对于多个福的情况,生成函数无非是多几个变量,往里代 \pm 1 的技巧是完全一样的。
再说说Markov过程的办法,实际上有这样一个结果,就是一个状态集的有限子集 S ,如果它是【封闭的】,也就是说从它出发到它外面的概率是 0 ,而且它是【可迁的】,也就是说这个子集中任意两个状态间在充分多步都有正的转移概率,那么从该子集开始者,最后一定会趋于稳定分布。最后如果它是【对称的】,即状态A一步到达B的概率等于B到达A的,这样稳定时落在每个状态的概率都是均匀的 1/|S| 。
利用这个结果,那么抛硬币就是两个状态,正面总量奇数和偶数。收集五福则要注意一下,因为题目问的是 2n 次抽取的极限,所以相当于一次开两个福。所以在总共奇偶的 2^5=32 种可能中恰好只有一半的情况是总量全为偶数的,剩下一半情况都是不会出现的,所以 |S|=16 ,于是最后的全偶概率就是 1/16 。
☆第七题,本题的背景是微分动力系统。只要写出来当前二人距离,到两个人各经过一次树下后新距离的函数,就会发现第一问的情况是,距离有一个不动点 d_0 ,然后距离 d<d_0 就会不断变小,距离 d>d_0 就会不断变大,因为圆周长是 1 所以最后距离变成 0,1 都算是两人相遇。
第二问懒得做了,摆烂了!!!实际上我在周日出去玩儿了,所以也没算最后一小问。粗看上去无非就像 x_{n+1}=\sin x_n 那道经典淑芬习题一样,只需要估个阶就完了,所以也不是很有兴趣和动力去做。
附上我的解答。