贴出来John椭球的参考文献是不是也能得点分(๑°3°๑)狗头
这次应该是当炮灰分母了!但我却十分乐意,甘当分母,壮个人气。这算是在中国由大企发起的数学竞赛活动,并且不限参赛者年龄身份,题目也偏应用趣味,这对于宣传推动数学发展是有积极意义的(要知道马云数学可是非常差的,正如他所说“外界一直传言,事实上也是真的,我第一次高考数学考了1分。这给社会上造成了误解,认为马云数学1分,照样成功了,所以数学不重要。其实我特别敬畏数学,数学非常重要!”)。希望更多企业能”达“后投身更多由意义有责任的事业中难去。
我是第一天下午抽了空做了选择题,第二天晚上才熬夜来做大题,所以后面神志不清,思维已经混乱了,解答有很多纰漏,还请看官不要较真。
也记录下小菜的答题过程吧。
1、我是这样想的,假定人只能看到ABCD4个塔,那么某个人看到E或F一定会被ABCD中某一个遮挡。假定1E之间被A遮挡,1F之间被B遮挡(EA\cap FB=1)。我们先按人数最多的情况例举:
EA\cap FB=1,EA\cap FC=2,EA\cap FD=3 \\ \underline{EB\cap FA=4},EB\cap FC=4,EB\cap FD=6 \\ \underline{EC\cap FA=7},\underline{EC\cap FB=8},EC\cap FD=9\\ \underline{ED\cap FA=10},\underline{ED\cap FB=11,ED\cap FC=12} \\
根据EF反向定位共12个人。这里已经忽略掉 EX\cap FX=1 定位一个人的情况,否则1和X重合了。注意到 EA\cap FB,EB\cap FA 是不能同时存在的,因此去掉下划线的人最多只能有6个人。
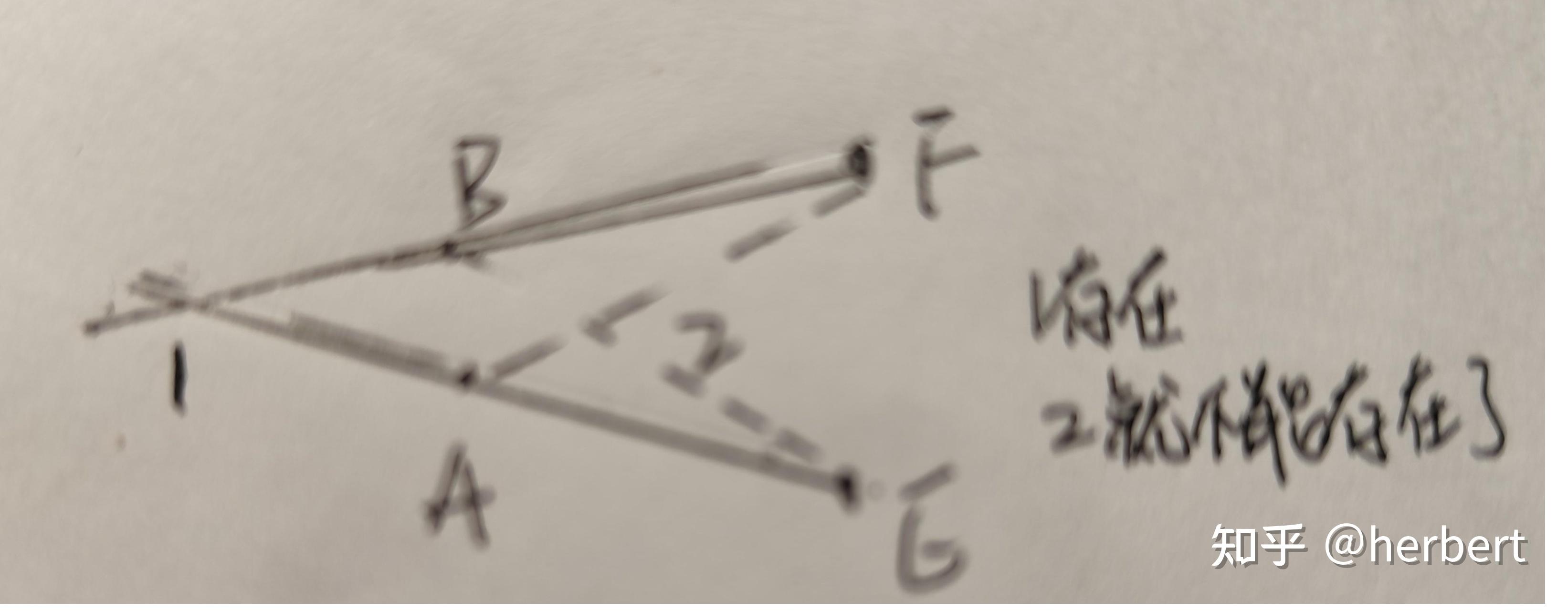
我们再按找刚刚的思路:由EF反向连线ABCD分别找到6个人找到存在的图形即可。
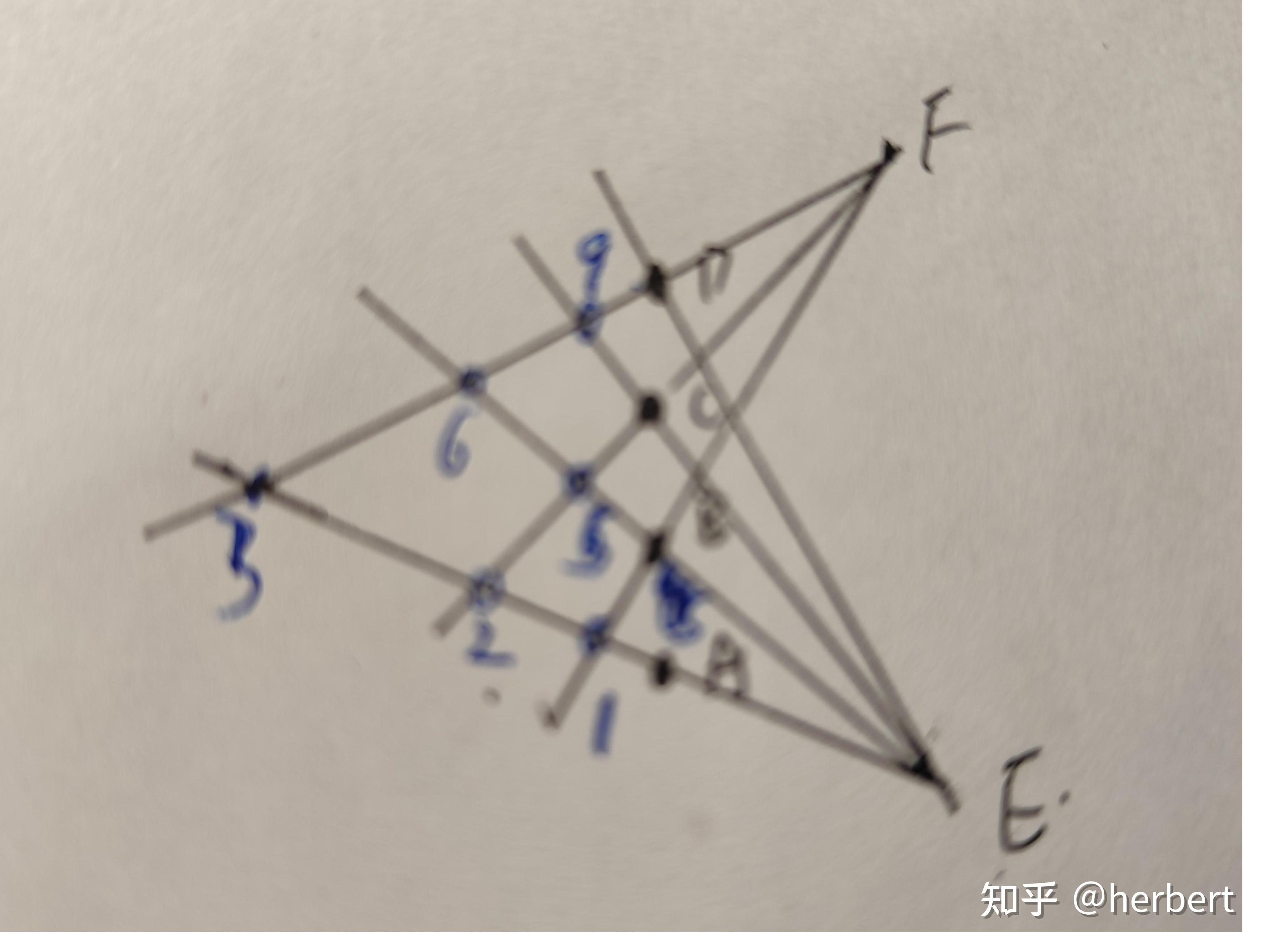
2、可以用微积分计算。当然我是直接写代码模拟的。第一问是2第二问也是2。实际上这题分数随时间衰减的太厉害了,而打下一架飞机只有1.5分,因此累积得分会衰减的很快,初步估计也是2-3次后不能继续玩了,因此也可以假设飞机每隔一秒来一次计算出累积得分,误差不大,也能得出结论(两种方式都模拟了)。
import numpy as np
def simulation():
scores = []
score = 2
successes = []
target = 0
time=np.random.exponential(scale=1, size=10)
for t in range(1,50):
# for k in range(len(time)):
# t=k+1
# score -= time[k]
score -= 1
if np.random.rand()<=0.85**t:
#击落飞机
score += 1.5
target +=1
scores.append(score)
successes.append(target)
return scores, successes
s=[]
n=[]
for i in range(1000000):
x,y=simulation()
s.append(x)
n.append(y)
s=np.array(s)
expect = np.mean(s,axis=0)
tries = np.mean(n,axis=0)总体而言,今年题不算难,但是选择题和趣味题变少了,有点让我这种凑热闹的感到可惜。
3、第一问还是比较简单的,可设 A=[a,c;b,-a] ,注意到 A^n 指数项为偶数时
是(a^2+bc)^{\frac{n}{2}}I ,奇数项是 (a^2+bc)^{[\frac{n}{2}]}A , |det(A)|=|a^2+bc| 即可带入计算.
第二问不太懂。。
4、也是高等代数。刚开始看到是三对角矩阵的行列式,以为特别简单,做后发现很难。当时猜测了下几个思路:
1)按行列式规则展开发现行列式与阶数间的递推式。没有找到。。本来题目已经告知特征值了可以猜出来特征多项式为 f(\lambda)=a(\lambda+d)(\lambda+d-1)\cdots(\lambda-d) ,然后伪证之或者用数学归纳证明结论的,但是当时太晚了,头脑不清晰,没精力去计算,不知道行的通不。
2)结合n多年前大一做题的经验,应该是要对矩阵做些行列交换,行列相加的操作,矩阵行列式的规律才看得出来。我只简单想了下,想不到,遂放弃。
3)因为之前有了解三对角矩阵的线性方程组的数值求解。我猜测可以借鉴里面的思维,需要把矩阵分解为LU或者 QDQ^T ,的方式其中D为对角阵,后去求行列式。我做了下LU尝试,没能成功,遂放弃。
第二问,完全不懂了,放弃。
5、实在不懂。当时我想到凸多面体的数学表达 Ax\leq b ,能不能构造一个椭球 xQx+cx+d=0 使得它上面的点全不满足上面不等式,且他被另外一个等比例放大的凸多面体包住的,这样他的体积就满足条件。但是实在想不清楚体积与表面积的关系,遂作罢。我也尝试搜到john ellipsoid的论文,但是不很准确,晚上也看不懂。不过有人找到下面这篇文章:
estimation of the convex polyhedron surface area using ellipsoid
6、概率题,比较简单。掌握二项式分布和多项式分布即可。当然我也想过能不能找到 P_{2n}=P_{2n-2}\cdots 的递推关系,其中 P_{2n} 有几种分布情况 P_{2n}^1:全部是偶数,P_{2n}^2:2个是奇数,P_{2n}^3:4个是奇数, 等,然后找到状态转移矩阵,对马尔科夫链求稳态即可。对我而言有点复杂,所以我还是仿照第一问的方式求解

