初学者或者外行人能理解的程度
让我们从微观世界说起。研究微观世界的问题需要用量子力学。而所谓的“量子”其实就是“一份一份”的意思。用生活中的例子来形象地比方可以用下图来说明。
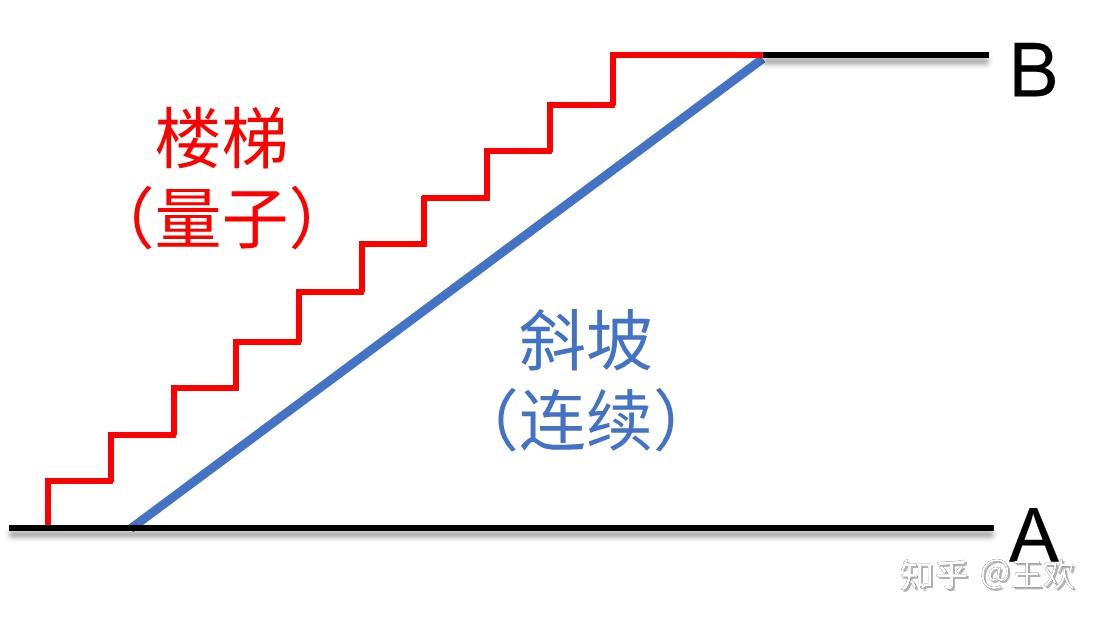
从图中可以看出,如果要从地面A来到高处B,我们可以有两种不同的途径:要么走斜坡,要么走楼梯。在斜坡上,每升高一段和之前的一段的高度差可以无限小,就是连续上升过程;而楼梯是通过一级一级的台阶上升,每两级相邻台阶之间高度差是有具体数值的,并不是无限小的,这就是所谓的量子化。
或者,我们可以用另一个模型(梯子)来说明。它和楼梯的台阶类似,同样是从地面A来到高处B,我们可以借助梯子来攀登,如下图所示。
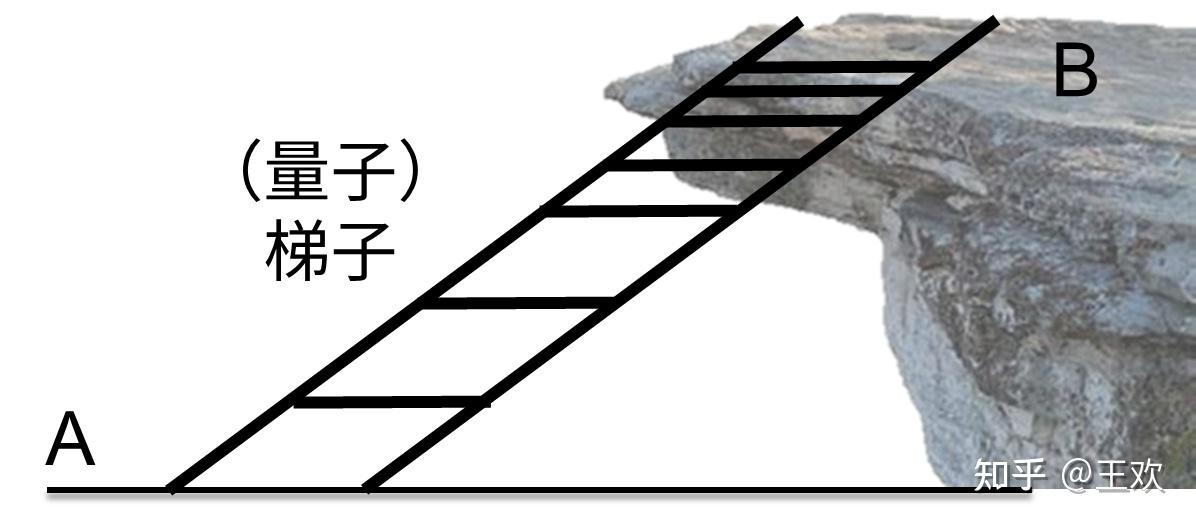
爬梯子也需要踩在梯子的横杆上,一级一级向上走:
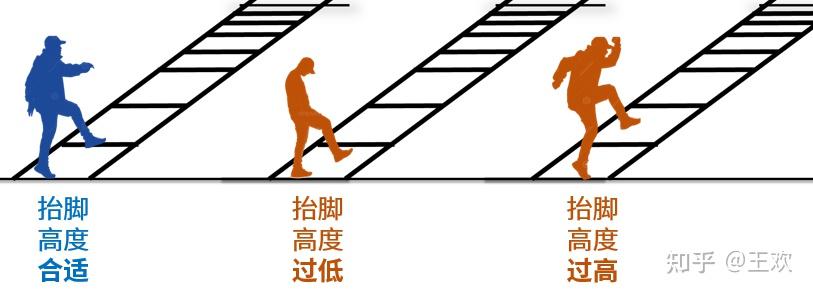
- 并且脚必须抬到一定程度正好踩在横杆上(如下图的左图),
- 如果抬脚太低则登不上横杆,也就无法登上梯子(如下图的中图);
- 另外,脚也不能抬得过高,即,踩在两个横杆之间,容易踏空(如下图的右图)。
有了上面这些感性的初步认识,就可以正式进入量子世界了。
物质是由原子构成的。组成物质的原子、分子这些微观物质遵循量子力学的规律,也就是说,它们的能量是一份一份的,就像上面给出的例子里楼梯或梯子的台阶。原子、分子中这样一份一份的能量,我们称之为“能级”。当其他物质的能量(比如光)与原子、分子相互作用的时候,能量的相互转换也遵循一份一份地吸收,或者发射。这就是爱因斯坦提出的 E=h\nu ,其中 E 是光的能量,或者称为光子的能量, h 是普朗克常数, \nu 是光子的频率。通俗地说,当光子的能量与物质(原子、分子)的两个能级之间的能差相等的时候,物质才能吸收这一份光子的能量。用公式来表达可以写成:
E_{光子}=h\nu=E_{能级2}-E_{能级1}=\Delta E=(吸收)峰在光谱中的位置
不同物质的能级差会不相同,所以吸收光子的能量会有区别,而不同能量的光对应着不同的频率(波长),这就是应用光谱来检测不同物质的最基本原理。上述基本原理可以应用于几乎任何以光作为检测手段的谱分析,例如紫外-可见吸收光谱,荧光发射光谱,红外吸收光谱,拉曼光谱等。只不过不同波段的光对应的能量不同,检测的对象对应的能极差不同,会从谱峰体现出不同的性质,但是原理基本相同。
稍进阶一些。
红外光谱、拉曼光谱统称为振动光谱,对应的是分子的振动信息。说白了就是分子中的各个原子之间的相对运动。科学家为了研究方便,将这些振动简化成了类似用“弹簧”连接在一起的小球的振动。
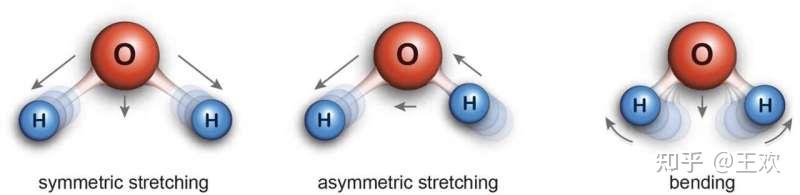
振动的样式不同(专业术语称为“振动模式”,vibrational modes),对应的能量也不同。这里的能量也和前一节说的能量一样是“量子化”的,也就是一级一级变化的。每一种振动模式对应的能量之间是分立的,不连续的,量子化的。也就是说,每一种振动模式在光谱上对应是分立的谱峰。这也是可以应用红外光谱、拉曼光谱检测不同物质的原因。
当然,当分子复杂了,振动模式将非常多,相互之间的影响也会更复杂,同类原子之间的振动能量也比较接近,于是光谱变得更复杂,谱峰之间也会有交叠,看起来也就不那么分立,不那么量子化了。
另外,溶剂分子(也就是所谓的环境)对待检测分子的振动也会有影响。简单地说,就像你平时走路没觉得空气对你有很大的阻力,但是在游泳池里走路就会觉得阻力很大,在游乐场的“海洋球”里走路又是另一种体验,也许以后载人航天普及了,在太空中行走又有不同体验一样,在不同的环境里,分子的运动会受到周围环境的影响,对应的振动峰也会有所偏移。
希望上面的科普性质的回答对你有帮助。