印度人说:我不同意,早在公元前1500年,我们印度人就用杠杆来提水和把士兵升到城墙之上,我们管这个装置叫dhenkli[1]。
古埃及人说:那是古印度文明,和你没什么关系,先坐下,记得死神阿努比斯的审判之秤么[2],其实我们早在公元前2200年就用杠杆了,我们管它叫shaduf(shadoof),后来才有了希腊人的klonion(kelonion)。

美索不达米亚人萨尔贡一世说:我们在征服苏美尔人的时候,就发现他们称之为zirigum的提水工具了,我还命人把它被刻在一个美索不达米亚的圆柱印章之上。
亚述人表示,那我公元前8世纪的事儿就不提了。

有人会说:不,不,不,那中国人在殷商还发明了筷子呢,筷子也是杠杆啊
确实,会用杠杆,就像会用桨划船,应用不代表你理解其原理。
那么,是谁先发现了杠杆原理的呢?
首先,我们看看《墨经》是怎么写的
(关于《墨经》的成书年代众说纷纭,目前主流观点认为《墨经》是墨后、也就是墨子之后的人写的,但不论怎么说,墨子比阿基米德(公元前287年—公元前212年)早生200年,所以本文倾向于《墨经》成书时间早于阿基米德的年代。另外,阿基米德有可能并没有说过“给我一个支点我能撬动世界”的话,目前所有证据都指向5个多世纪之后古希腊数学家帕普斯写在《数学汇编》里的引文,相当于今天突然有人写“1490年一个名人说过”,这在高考作文卷上更常见)
《墨子 · 经下》中是这样描写的:
“衡而必正,说在得”;“衡,加重于其一旁,必捶,权重不相若也,相衡,则本短标长,两加焉,重相若,则标必下,标得权也”。
衡,就是秤杆;权,就是秤砣;“权衡轻重”就是这么来的。
这段大致意思就是:
秤杆要保持平衡,关键是有一个可以滑动调节的秤砣。保持平衡的秤杆一头如果加上重物的话这头就会降低,这是因为重物和秤砣(的力矩)不相等了。如果要保持平衡,就要挂重物的一端短,挂轻的秤砣的一端长。
再看看阿基米德是怎么写的

阿基米德在《论平面图形的平衡(On the equilibrium of planes )》第一卷第6、7节中写的[3]意思大概是:
距离相同处的等重物体处于平衡状态,而距离不同处的等重物体处于不平衡状态并会向距离较远的物体一侧倾斜[4]。
读到这里,你会发现,阿基米德说的和墨经里说的是差不多的意思嘛,这个道理估计商代挑扁担的老农也能略懂一点,只不过没有形成文字罢了。
但接下来,阿基米德没有止于“经验”,而是想把它变成后来康德所说的“先验”。他觉得这个现象背后的原因是酱婶的:
让我们做一个思想实验,当质量分别为2公斤和3公斤的重物以3米和2米的距离平衡时:
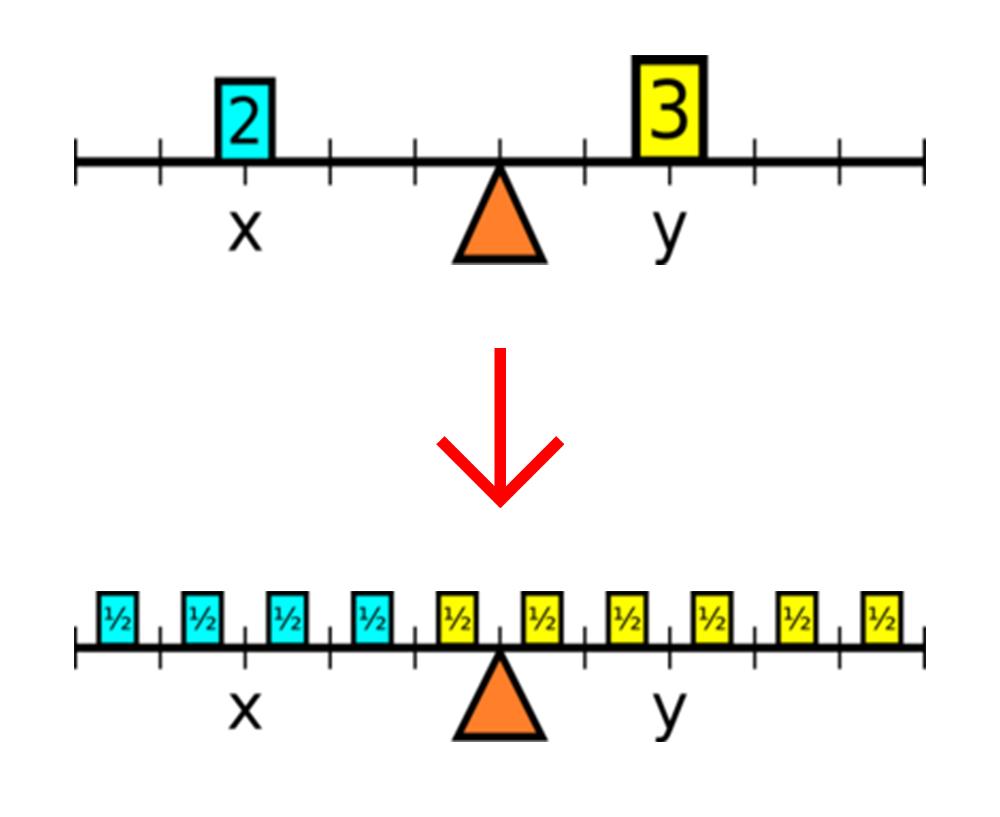
他把重量均分在了整个杠杆上,蓝色与黄色就变得“自然而然、显而易见、不证自明”的平衡了,此时新的重心与原来的重心没有区别。
阿基米德试图在几乎没有任何物理理论支持的情况下证明杠杆定理。他从等距等重平衡的假设中,直接推导出了重量与杠杆臂成反比。
尽管从现在的角度来看,这个证明是有瑕疵的[5],但至少是想从数学的角度来解释这一问题。事实上,在阿基米德出生之间,逍遥派(Peripatetic School,亚里士多德弟子组成的学派)就曾发表过一本名为《Mechanica》[6]的书,其中就已经提到:
杠杆(两端)移动的幅度、以及重量之比,反比其离中心的距离[7]。
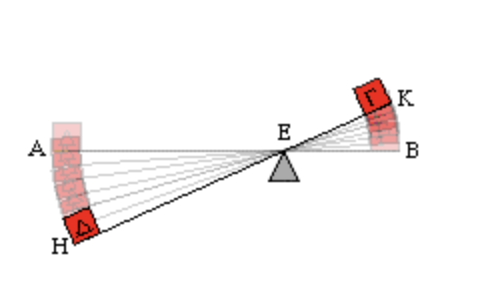
所以不难看出,相比于墨子的定性分析,从古希腊的先哲们的定量分析中想要推导出 m_{1}\times L_{1} = m_{2}\times L_{2} ,也就是我们现在所说的“动力×动力臂=阻力×阻力臂”这一概念,应该更直接一些。
一些思考
单看独立的命题,中国某些古人的数学很厉害,从勾股定理到圆周率,都有着光辉的一页;
但从整个体系来看,中国古代对数学体系几乎没什么帮助。从阿基米德到庞加莱、从大学里学习的高数线代微积分、到数分复变拓扑学,背后是一套完整的数学体系。
数学,不是只发现一两个值得骄傲的现象和定理就能建成大厦的。
现在中国强大了。以前我小的时候,看着写满外国人名的定理(插一个题外话:大多数定理都不是定理名字里的那个人首先发现的),那时候我听到最多的情绪输出就是:“我们曾经也有过”、“我们才是第一个发现的”。
但却从没有人告诉我,数学结论只能从逻辑出发,要经过假设、演绎、推理和论证后得出结论。
有了逻辑,后人才能沿着前人的脚印继续在批判中前行,才能创造出持久辉煌的科技文明。
所以,这不是阿基米德与墨子间的博弈,也不是什么崇洋媚外谁的月亮更圆,而是传统中国人讲究周易思维,是模糊而灵活的。
但现代科学只讲究“逻辑”。
参考
- ^https://rezavisblastfromthepast.co.in/2018/04/30/the-early-waterlifting-devices-dhenkli-or-shaduf-and-the-araghatta-noria/
- ^严格地说,“秤”应指不等臂秤,而“天平”才代表等臂秤。
- ^Magnitudes are in equilibrium at distances reciprocally proportional to their weights.
- ^ ARCHIMEDES by E.J. Dijksterhuis (translated by C. Dikshoorn) Princeton University Press, Princeton, N.J., U.S.A., 1987
- ^George Goe, Archimedes' theory of the lever and Mach's critique, Studies in History and Philosophy of Science Part A, Volume 2, Issue 4, 1972, Pages 329-345, ISSN 0039-3681, https://doi.org/10.1016/0039-3681(72)90002-7.
- ^ARISTOTLE: MINOR WORKS Translated by W. S. HETT Loeb Classical Library Harvard University Press, Cambridge, 1936 Volume XIV, Mechanical Problems, 3, Pages 353-355
- ^https://math.nyu.edu/~crorres/Archimedes/Lever/LeverLaw.html