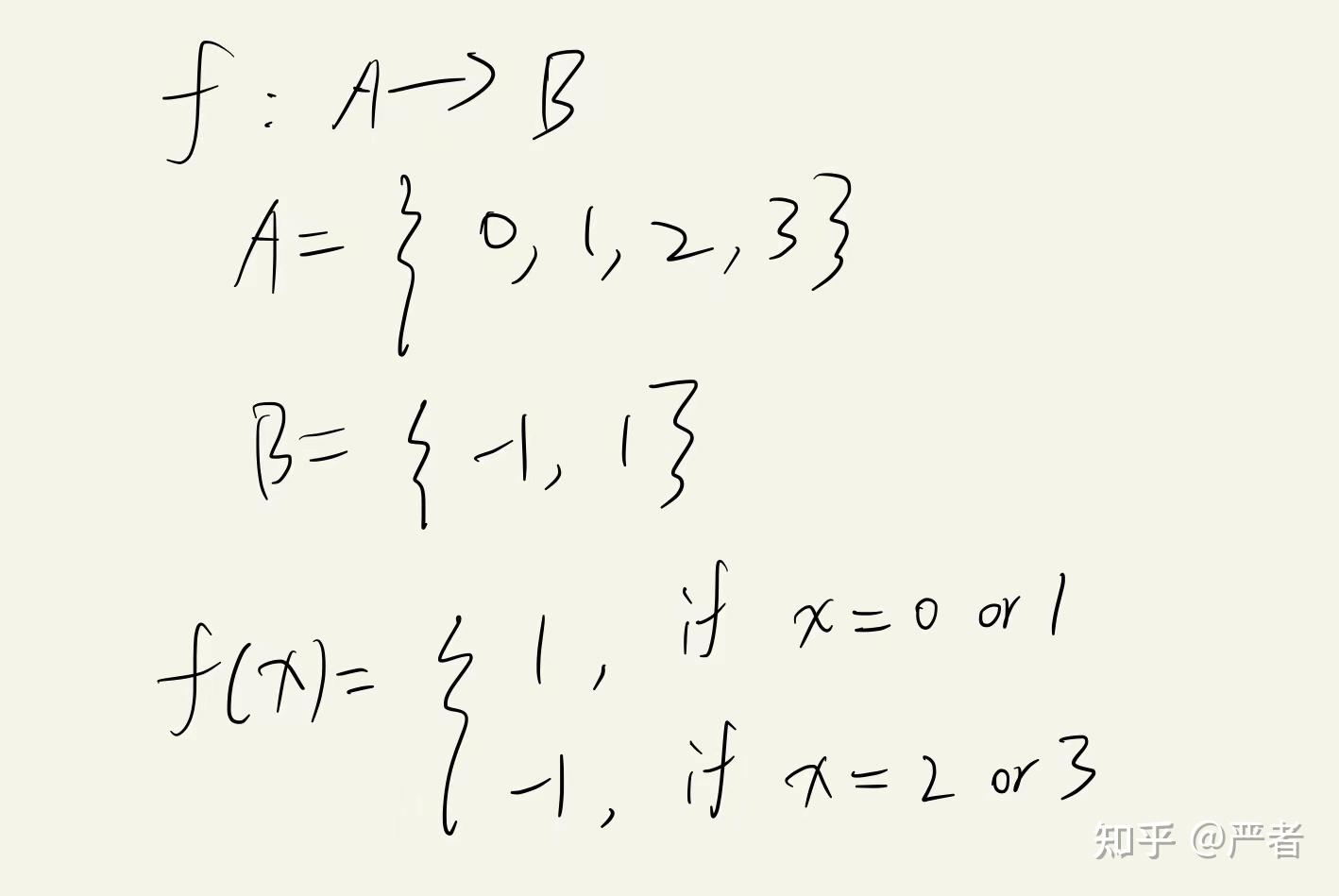一

首先，拉格朗日插值法永远是您最可靠的选择，构造函数

$f(x)=\frac{(x-1)(x-2)(x-3)}{(0-1)(0-2)(0-3)}\times1+\frac{(x-0)(x-2)(x-3)}{(1-0)(1-2)(1-3)}\times1+\frac{(x-0)(x-1)(x-3)}{(2-0)(2-1)(2-3)}\times(-1)+\frac{(x-0)(x-1)(x-2)}{(3-0)(3-1)(3-2)}\times(-1)$f(x)=\frac{(x-1)(x-2)(x-3)}{(0-1)(0-2)(0-3)}\times1+\frac{(x-0)(x-2)(x-3)}{(1-0)(1-2)(1-3)}\times1+\frac{(x-0)(x-1)(x-3)}{(2-0)(2-1)(2-3)}\times(-1)+\frac{(x-0)(x-1)(x-2)}{(3-0)(3-1)(3-2)}\times(-1) 有种简单的美。

二

当然，拉格朗日是无法满足简单这个条件的，在此，我们可以构造三角函数

$Asin(ωx+φ）$Asin(ωx+φ） ，代入这四个点，得出一个函数

$f(x)=\sqrt{2}sin(\frac{\pi}{2}x+\frac{\pi}{4})$f(x)=\sqrt{2}sin(\frac{\pi}{2}x+\frac{\pi}{4})

也是所求

三

或许三角函数还不够简单，我们可以用绝对值函数来试试。

先求出过 $(1,1);(2,-1)$(1,1);(2,-1) 两点的直线为 $y=-2x+3$y=-2x+3 ，再将函数斜率的两个转折点 $x-1=0;x-2=0$x-1=0;x-2=0 写成绝对值，

设所求为 $a|x-1|+b|x-2|$a|x-1|+b|x-2| ，则在 $[1,2]$[1,2] 区间内， $a(x-1)+b(2-x)=-2x+3$a(x-1)+b(2-x)=-2x+3 ，则 $a=-1;b=1$a=-1;b=1

所以，所求为 $-|x-1|+|x-2|$-|x-1|+|x-2|

最简单的当然是用分段函数。

但是我想想个办法用算术运算模拟逻辑运算，再把逻辑运算还原成算术运算。

挖坑待填。

$f(x)=\sqrt{2}\sin \left(\frac{x\pi }{2}+\frac{\pi }{4}\right)$f(x)=\sqrt{2}\sin \left(\frac{x\pi }{2}+\frac{\pi }{4}\right)

这个公式的图形应该是

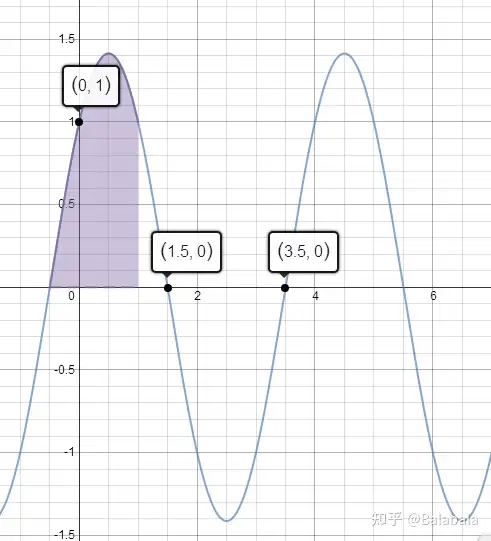
满足f(0)=f(1)=1，f(2)=f(3)=-1