如何证明“若A是可逆矩阵，则A可以表示成有限个初等矩阵的乘积”？

首先，需要明白对于矩阵作初等行变换相当于左乘初等矩阵，作初等列变换相当于右乘初等矩阵。

其次，所有的初等矩阵都是可逆矩阵。

由于矩阵 $A$A 可逆，设其标准矩阵为 $F$F ，则 $F$F 必然可以通过有限次初等变换成为 $A$A 。

则有 $A=E_1E_2...E_rFE_{r+1}E_{r+2}...E_{t}$A=E_1E_2...E_rFE_{r+1}E_{r+2}...E_{t} ，其中 $E_{1}，E_{2}，...，E_{t}$E_{1}，E_{2}，...，E_{t} 均为初等矩阵。

由于 $A$A 为可逆矩阵，$E_{1}，E_{2}，...，E_{t}$E_{1}，E_{2}，...，E_{t} 也为可逆矩阵，则 $F$F 也为可逆矩阵。

则 $F$F 为单位矩阵 $E$E （初等矩阵），则可逆矩阵 $A$A 可以表示为若干个初等矩阵的乘积。

或者等价表述为若矩阵 $A$A 可逆，则 $A$A 一定可通过有限次初等行变换化为同阶单位矩阵 $E$E 。

这个结论的主要用处是：由于 $E_1E_2...E_kA=E$E_1E_2...E_kA=E 且 $A^{-1}A=E$A^{-1}A=E ，

则有 $A^{-1}=E_1E_2...E_k$A^{-1}=E_1E_2...E_k ，两侧同时右乘矩阵 $E$E 也有$A^{-1}E=E_1E_2...E_kE$A^{-1}E=E_1E_2...E_kE

即有 $A^{-1}=E_1E_2...E_kE$A^{-1}=E_1E_2...E_kE 。

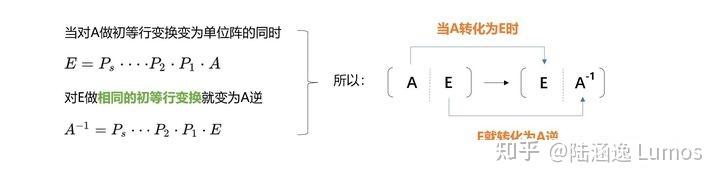
所以在计算某个矩阵的可逆矩阵时可以在其右侧拼上一个单位矩阵，同时作初等变换。

这样在矩阵 $A$A 变换为 $E$E 的同时，矩阵 $E$E 就会变为 $A^{-1}$A^{-1} 。