爱因斯坦,终究还是输给了玻尔。
也就是说,任何形式的「定域隐变量理论」,都是不可能的。
我用「类比」的方式,给数理基础较弱的朋友,说说「量子纠缠」。
先借用一下大家的「手套」。
比如说我们有一双手套。
我们秘密地,将这一双手套,分别放到两个箱子里。
没有任何人知道,哪一个箱子里,放的是哪一只手套。
我们这时候把一只箱子留在身边。
另一只箱子快递到地球的另一面。
比如说华盛顿,给钢铁侠。
钢铁侠打开箱子一看。
咦,是左手。
那么他立刻就知道,你这边的箱子里是右手。
哪怕是相隔万里,他对你这边箱子的认知也是瞬间的。
这个并没有任何奇怪之处 —— 如果我们用经典的思维来看的话。
经典思维里,当我们把手套放在箱子里的那一刻,每个箱子里的手套是左、还是右,事实上就已经确定了。
我们不确定,只是因为我们不知道。
但是箱子里的手套的状态,却是确定的。
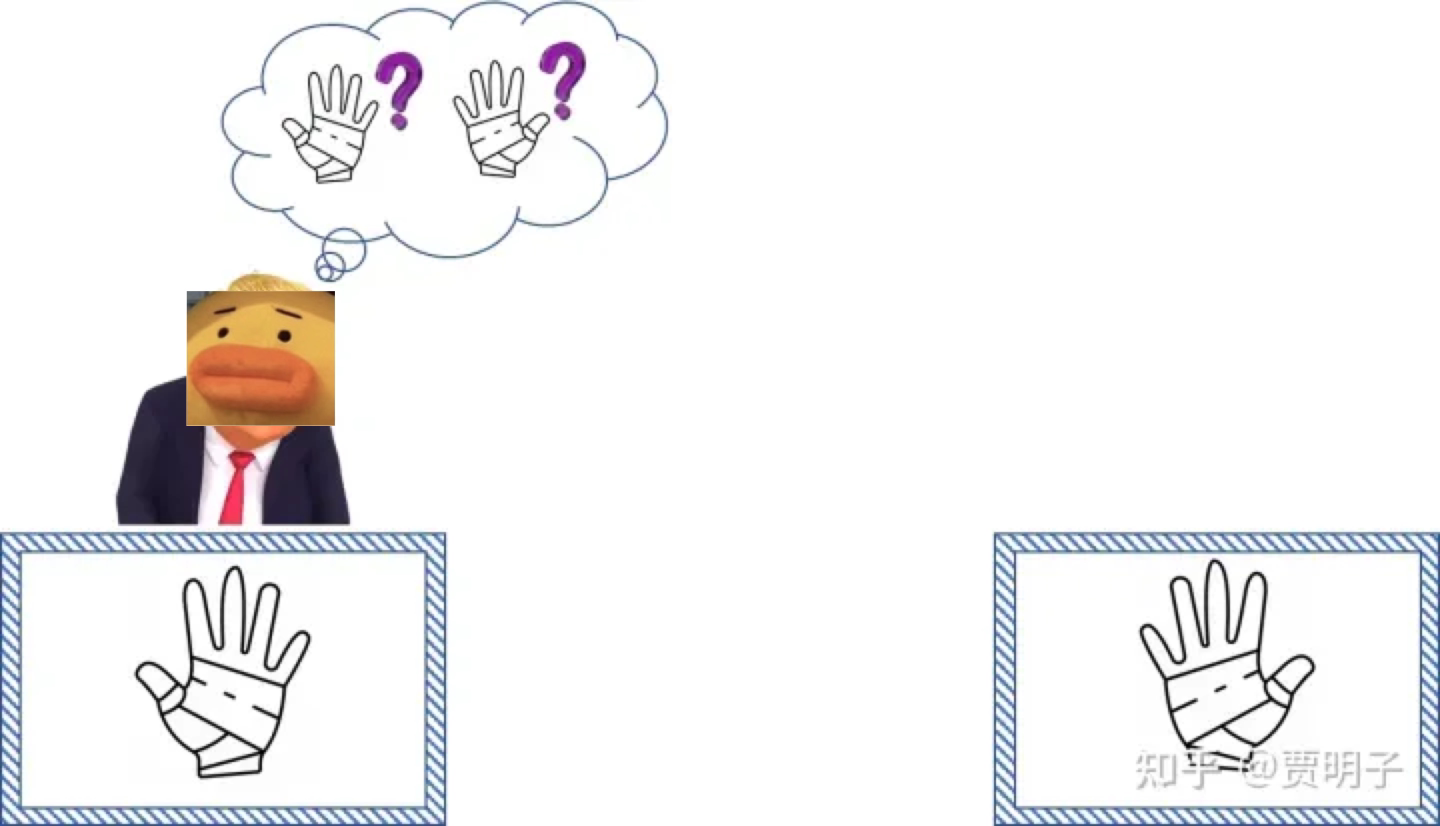
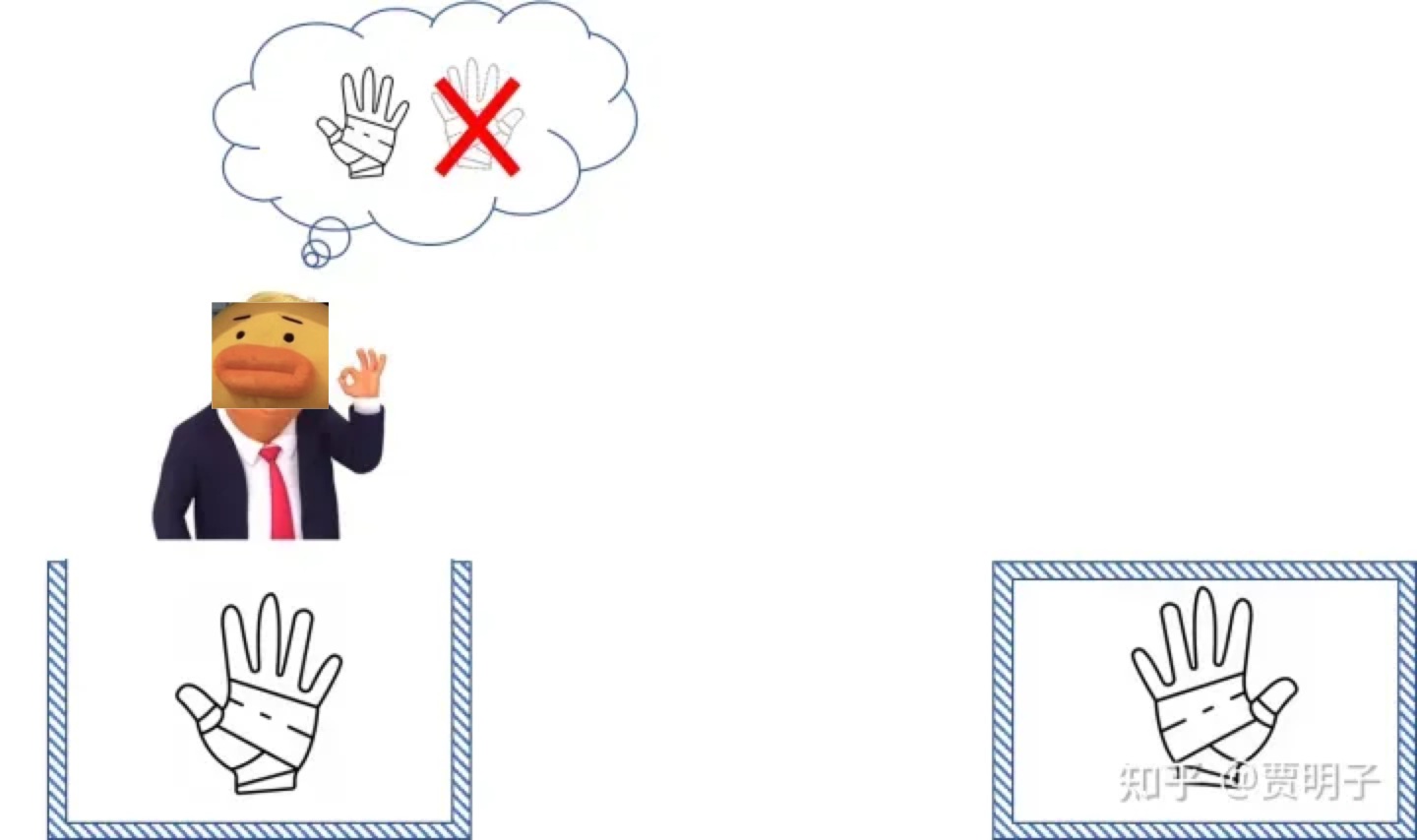
当箱子送给钢铁侠的时候,他打开一看,知道了是左手。
那么,他立刻知道另一只箱子里是右手。
这个过程中并没有发生任何奇怪的事情,诸如「远距离瞬间影响」之类的。
因为这中间的一切确定和不确定,都是发生在钢铁侠的脑子里。
而箱子里的手套,从头到尾都是确定的。
但是,如果箱子里面的是一双「量子手套」,它们像微观世界一样有着种种量子性质。
当它们形成纠缠的时候,并不是像上面那种情况 —— 即箱子里的手套是确定的,只不过我们不知道。
而是说,箱子里的手套处于一种左手和右手的叠加态。
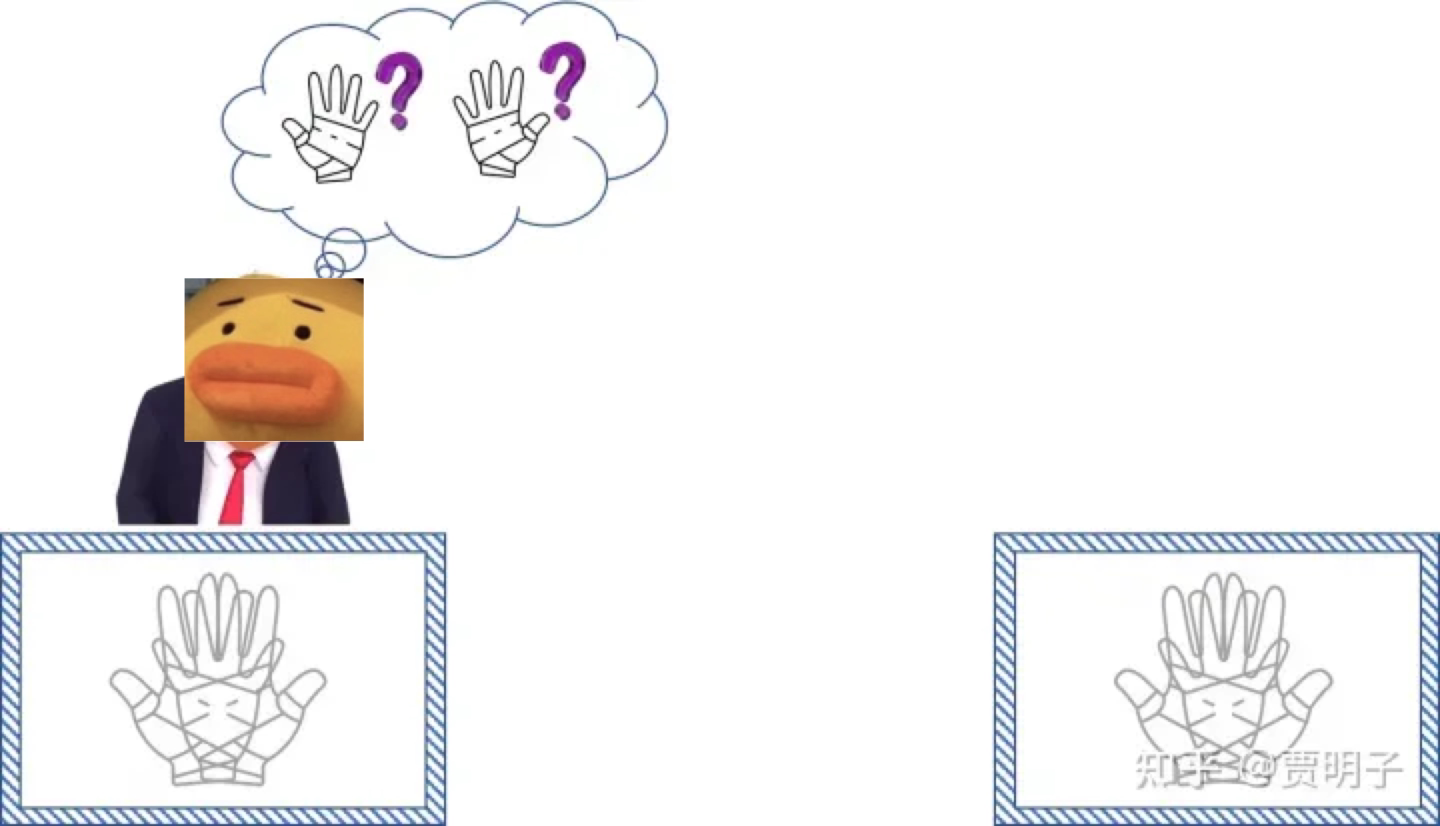
这个时候,钢铁侠当然不知道当他打开箱子的时候,会看到左手还是右手。
但是和经典情况不同的是,此时不光钢铁侠不知道,箱子里的手套本身也并不是确定的左手或右手,而是不确定的。
这一点从我们的日常经验看来,会觉得很荒谬。
但是在量子力学中,这种「左右叠加态」却是一种最基本的性质。
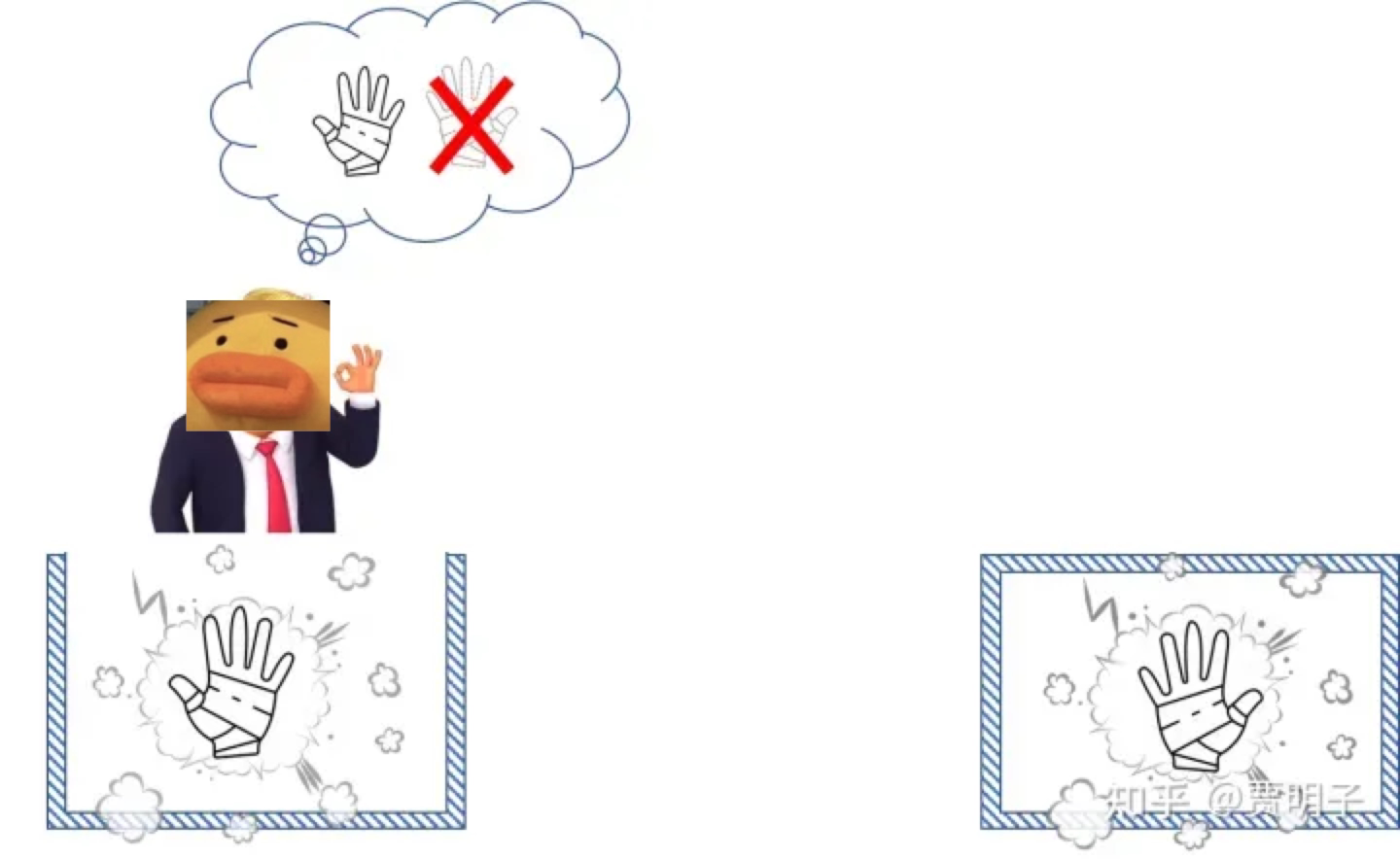
当钢铁侠打开箱子观察的时候,他看到了左手。
此时,箱子里的手套的叠加态就「砰」地在观察的瞬间「坍缩」成了一种确定的状态。
而在这个瞬间,他立刻知道了我们这边的箱子里的手套探索成了右手。
也就是说,他那面的观察行为导致的「坍缩」瞬间跨过万里,使得我们这边箱子里的手套从叠加态变成了右手态。
这里的确定性和不确定性,不仅仅是发生在钢铁侠的脑子里,而且是切切实实地发生在手套本身——
它从「叠加态」,向着确定的「左手」或「右手」的变化。
于是,爱因斯坦就问:凭什么打开箱子的瞬间,就能让万里之外的另一只箱子里的手套,发生这种巨变?
爱因斯坦就把这个叫作「spooky action at distance」,意即「远距离的幽灵般的相互作用」。
隐变量和定域性
上面的两种「手套」,有一个根本性的不同。
在第一种情况下,手套存在着一种我们不知道的确定的状态。
而在第二种情况下,手套则不存在这种确定的状态。
爱因斯坦说,量子理论必须要使用「叠加态」这种描述方式,是因为量子理论本身不是终极理论,或者说它是「不完备」的。
系统在我们尚未观察的时候,应该存在着确定的、隐藏的、不为我们所知或者尚未被我们知道的状态。
量子理论只是一个暂时的理论,现在对这种隐藏的状态无能为力,所以只好用表象的「叠加态」这种概念。
那么这种尚未被很好地描述的确定状态,是什么呢?
既然这种状态被隐藏在比量子理论更深层的部分,爱因斯坦就把它叫作「隐变量」。
所谓「变量」,意思是对于任何一种状态,我们都需要某种变量来描述它。
爱因斯坦说,没错,量子理论可以很好地解释很多现象,预测很多现象,它是成功的。
但是,它对这种隐藏的状态,也就是隐变量,无能为力。
所以它是不完全的理论。
物理上,叫作不完备的。
我们完全可以在实用的角度,来使用量子力学。
但是,我们不应该满足于量子理论。
我们要寻求更加基本的,能够描述隐变量的物理理论,也就是隐变量理论。
从上面的例子中我们可以看出,当我们假设隐变量存在的时候 —— 也就是假设一个不为我们所知的确定的状态存在 —— 整个过程就没有任何问题。
但是如果我们认为隐变量不存在,那么我们就面临着「在华盛顿发生的事情,瞬间影响到北京的事情」这种事情了。
可相对论却说,任何相互作用都是定域的。
所谓的「定域」,指的是一个事件,所产生的影响是在时空中向外以一定的速率传递的。
比如说,你和我打电话,你的声音被手机的麦克转变为电信号。
接着通过调制,以电磁波的形式传播到基站。
再接力传递到我这边的基站。
然后传播到我的手机里。
我的手机经过放大,通过音频设备转换成声音。
最后让我听到。
这是一步步传递过来的。
而不是说你那边说一句话,不经过任何通道瞬间就到我这里来了。
相对论说,任何信号和相互作用传递的速率不会超过光速。
这就叫定域性。
爱因斯坦说,第一种情况下,现实性(也就是说存在一种不依赖于观察者的确定的状态)和定域性(相互作用的传递是有速度的)都没有问题。
按照经典图景的看法,这个过程是没有任何「瞬间影响」的。
原因是,两个手套的不确定性只是因为我们的无知造成的:它们都有确定的「左手」或「右手」的状态,只是我们不知道而已,并不是它们真的不确定。
我们观察左手,得到确定的信息后,同时改变了另一只箱子里的概率。
但是,这个瞬间发生变化的只是我们对手套的知识,而不是手套的状态。
而第二种情况下,它们就都有问题了。
因为物体的状态,取决于观察(观察会让叠加态「坍缩」),而且有远距离瞬间的影响。
而两只手套的叠加态,就是它们状态的全部。
当左手坍缩时,右手的改变,是其量子态实实在在的改变。
因而,我们对左手的改变,实实在在地瞬间改变了右手的状态。
但对爱因斯坦来说,无论是客观性,还是定域性,都是无比重要的。
因此,他坚定地认为,量子理论是不完备的,一定有一种隐变量理论满足定域性和现实性。
EPR 佯谬
上面的只是一个形象的例子。
下面我们把手套换成粒子,把「左右」换成「自旋」,就是著名的 EPR 佯谬了。
物理学史上,真正把这种非定域性的效应明显地呈现在我们眼前的,就是这个 EPR 佯谬。
在石破天惊的 1935 年,爱因斯坦以他超凡的洞察力,对量子力学发起了最为致命的最后一击。
这一击,把量子力学最为尖锐的矛盾,也是最为奇葩的一面暴露在了物理学家的面前。
就是非定域性和实在性之间的矛盾。
下面我们一起看一看这个著名的 EPR 佯谬。
在这里,量子纠缠有史以来第一次明确地展现在世人面前。
EPR 三个单词,是三个人名字的组合,爱因斯坦(Einstein)和他的两位博士后助理,Boris Podolsky 和 Nathan Rosen。
在 1935 年,三人发表了一篇论文。
题目叫 「量子力学对物理现实的描述是完备的吗?」(Can Quantum-Mechanical Description of Physical Reality Be Considered Complete?)。
对于量子理论对物理实在描述的完备性,提出了强有力的质疑。
值得一提的是,EPR 中的另外两位,虽然在这个话题中,不幸掩盖于爱因斯坦的巨大阴影中,也都不是凡人。
其中 Rosen 很著名的贡献就是提出了「虫洞」理论(这无论放在物理学史的哪一个阶段,都是一个了不起的发现)。
而 Podolsky,据证实是苏联的克格勃。
在这篇论文里,爱因斯坦定义了如下的「现实性」:
「If, without in any way disturbing a system, we can predict with certainty (i.e., with probability equal to unity) the value of a physical quantity, then there exists an element of physical reality corresponding to this physical quantity.」(如果在不干扰系统的情况下,我们可以确定地预测某物理量,那么存在着某种物理现实和该物理量相对应。)
而「物理量对应着物理现实」这一点,在爱因斯坦看来,是必须的。
当然众所周知,这篇论文中的核心思想,全部出自爱因斯坦。
但是因为当时爱因斯坦的英文水平还很不行,所以文章是 Podolsky 执笔写的。
并且在提交之前,爱因斯坦并没有阅读过。
事后爱因斯坦对论文的表述表示了一些不满意,认为它画蛇添足地讨论了一些无关主题的东西,使得真正的主题反而有些模糊。
直至 1951 年,玻姆提出了他的版本的 EPR 佯谬。
他用「自旋 1/2」系统,简单明了,成为我们现在最广为人知的一种版本。
这里我们略过最初的 EPR 版本,直接谈论玻姆版的 EPR 佯谬。
「自旋」是微观粒子的一个独特现象,这在我们宏观世界中是不存在的,并且很难以用宏观现象来直观想象。
最接近的类比,就是一个旋转的小球。
虽然它和微观粒子的自旋,有着种种显著的不同,但是现在我们暂时用它来类比还是可以的。
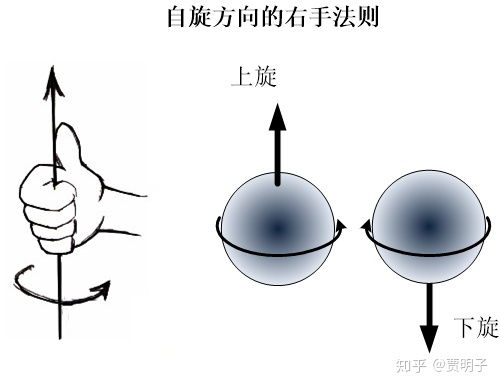
一个旋转的小球,它可以有不同的旋转方向。
比如从一个方向上看去,它可能是顺时针旋转,也可能是逆时针旋转。
因为顺时针和逆时针,从不同的方向看过去,是不同的。
因而物理学里面不用这种称谓,来区别旋转方向。
而是用一个叫作「右手规则」的方式,来规定自旋的方向为「向上」或「向下」。
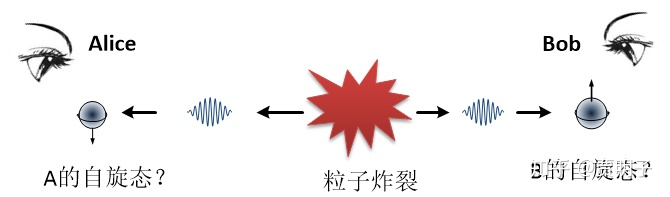
EPR 佯谬是一个思想实验。
在这里,我们设想一个静止的、没有自旋的粒子突然发生了一个爆裂,分成了两个相同的粒子 A 和 B。
然后这两个粒子向着两个相反的方向离去。
整个过程我们对它不进行观测。
直至 A 跑到宇宙的边缘,而 B 跑到宇宙的另一端。
这时候有两个人,分别在两端等着,A 这边是 Alice,B 这边是 Bob 。
然后他们都在同一个方向上对这两个粒子分别作出观测,结果会是怎样?
物理学中有一个普适的基本定律,叫作角动量守恒定律。
这个定律指出,孤立系统的总角动量保持不变。
角动量,是一个旋转的「强度」的度量。
既然一开始的粒子没有自旋,那么它分裂成两个粒子之后,两个粒子就必然会把整体的自旋抵消掉,。
也就是说,A 和 B 的自旋方向必然是相反的。
这件事可以说是非常古怪了。
你可能会觉得:这简单得很啊,哪里来的古怪?
且听我细细道来——
按照经典图景来理解,这件事当然没有什么可奇怪的:
粒子分裂成为两个自旋相反的粒子,然后这两个粒子就保持着自旋的状态一直到了 Alice 和 Bob [1] 那儿,这没毛病。
你只需要把粒子当作经典的小球就可以了——
两个人观察到的结果总是相反的,是因为这两个粒子本来就是以相反的自旋产生的。
它们从在一个粒子分裂出来的时候起,一直就是相反的。
在我们观察它们之前,我们只是不知道它们各自是什么状态罢了。
但是我知道,即使我不观察,它们的自旋也总是相反且确定的。
不过,按照量子力学的思维,古怪之处就来了......
