大家可以去看看楼红卫的《微积分进阶》
我真的无法用言语形容这本书的牛逼之处!这本书修正我的数学品味!
告诉我技巧的选择,应该优先正面硬上的一般通法,哪怕过程看着不那么简洁!
在我看了这本书之后,我才明白那些大佬被推荐的好书为什么牛逼?(我之前认为:题目难/看的门槛高/有很多高级知识...那就是好书了)我知道我想要什么知识了;我学会了筛选书/笔记/题目(这本书让我变成了伯乐),我发现那些之前看着“高大上”所谓的名校考研题期末题/考研满分笔记原来那么普通!
我再回看我笔记里的题目,我明白为何换个花样我就不会了,因为我只会背答案/技巧,但我背的技巧不具有普适性!我发现根本没真正看懂答案(“注意到”,自然而然的答案)我开始重新思考答案的整体思路是什么?怎么思考出来的?思路能不能推广?条件能不能减弱?凭什么注意到?我搜过论文/辅导书/问过别人,最终得到的只是冰冷的标准答案!我把可能是同一类型的题目归类,一遍又一遍看答案,终于想出来了一些原因,再用各种题目测试,终于,我有了自己的原创总结!有了能“通杀”这类题的方法!


指引你去寻找答案!要/应该思考什么?如何发现问题/研究方向?

我从未在任何一本辅导书见过下面的细节解释!我还是太天真了!

微积分进阶PDF:https://mp.weixin.qq.com/s/VWPoFY086LkfiCnKITvwzQ
另外分享一本书——《线性代数的艺术》,一共只有12页纸,而且一半都是图解,小白也不用担心看不懂!
现在,这份笔记在GitHub已经获得了4k+次星标,还登上了热榜。
这份笔记是基于MIT大牛Gilbert Strang教授的《每个人的线性代数》制作的。
《线性代数的艺术》完整版PDF:https://mp.weixin.qq.com/s/VWPoFY086LkfiCnKITvwzQ

日本学者Kenji Hiranabe把这部368页的巨著浓缩成图解,制成了这套笔记并免费开源,后被国内网友kf liu翻译成了中文。
结果不仅在GitHub上反响很好,还得到了原作者的肯定,被收录进了原书介绍页面的interesting link。
甚至Strang还为这份笔记题写了一段前言。

下面就来一起看看这份被原书作者点赞的笔记都讲了些什么吧!
内容介绍
正式进入这份笔记的主体之前,我们先来看看线性代数的世界是什么样子的~

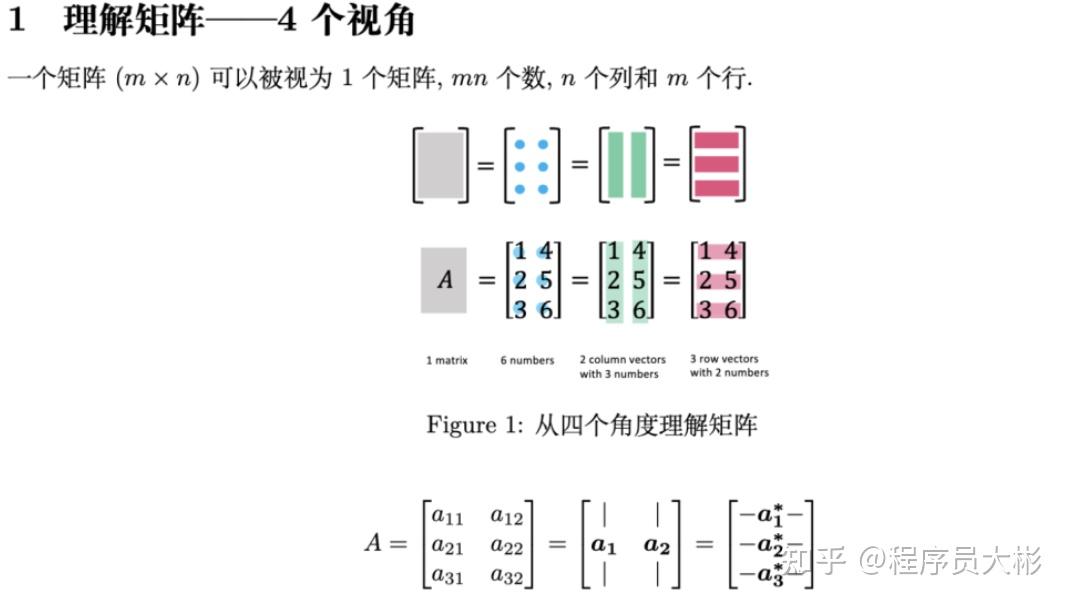
从这张图中我们不难看出,有关线性代数的一切都离不开一个基本概念——矩阵。
因此这份笔记正是从理解矩阵开始的,在这一环节一共展示了4个视角。
有了矩阵的概念之后,作者接着由浅入深地介绍了一些运算方式。
作者依旧是用图的形式讲解,并从不同的视角进行分析,具体包括:
- 向量乘向量
- 矩阵乘向量
- 矩阵乘矩阵
这里我们展示一下最简单的向量乘向量:

基本的运算方式往往是最正确的,但不一定是最高效的。
所以这份笔记接着展示了一些实用技巧。
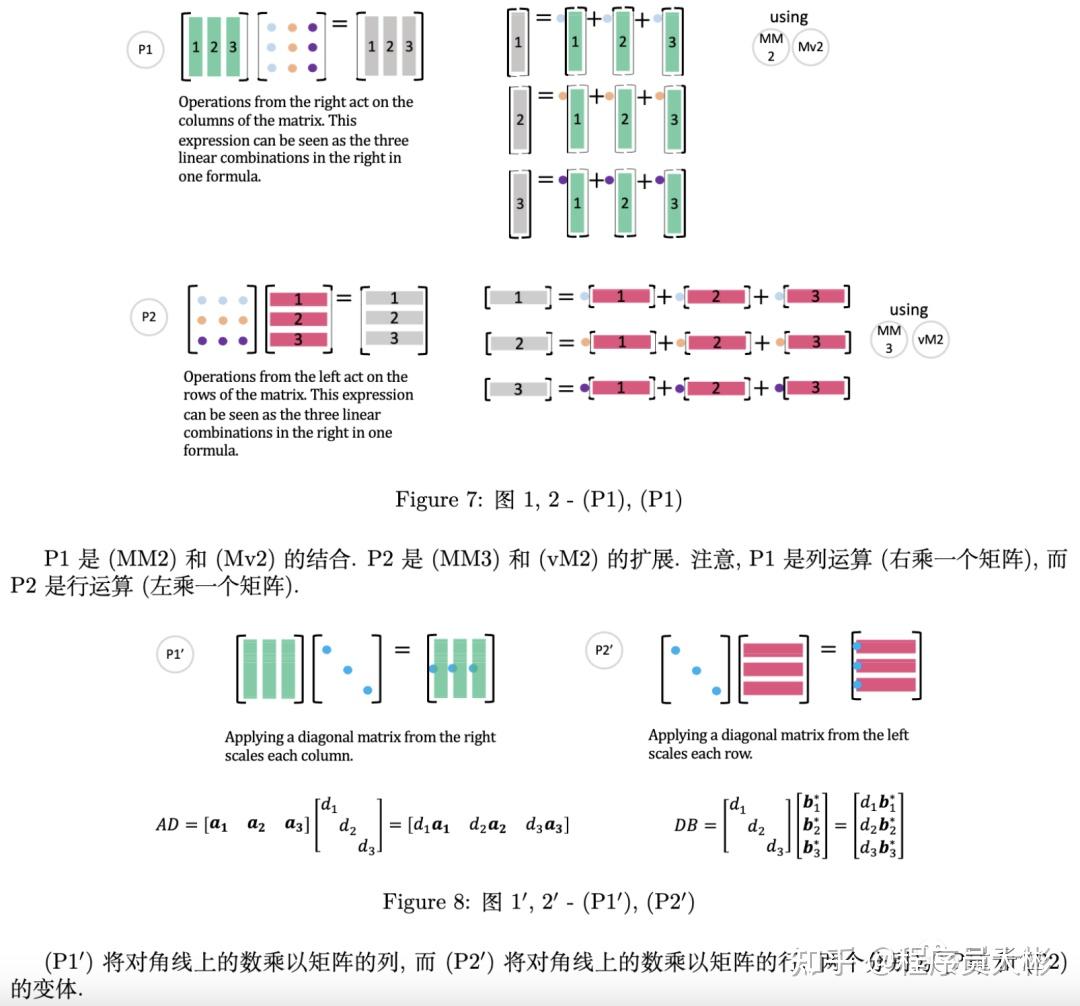
这项技巧还可以用于微分方程的求解。
此外,这份笔记还介绍了矩阵的五种分解方式:

针对以上每种分解方式,还有具体的讲解:

笔记的最后,作者还附上了一张矩阵的特征值映射图。
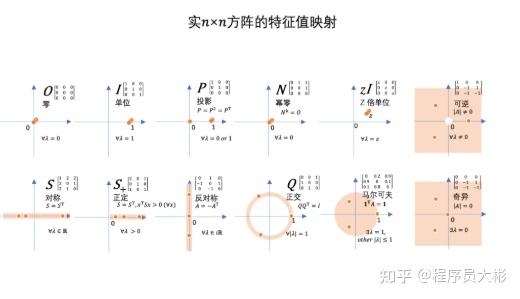
怎么样,看了之后是不是感觉很容易理解?
附上《线性代数的艺术》完整版PDF:https://mp.weixin.qq.com/s/VWPoFY086LkfiCnKITvwzQ