举一个最简单的例子,马其顿长矛15米这个问题。
伪史论者自称,他们是为了对抗那些一说起马其顿长毛就15米的人。
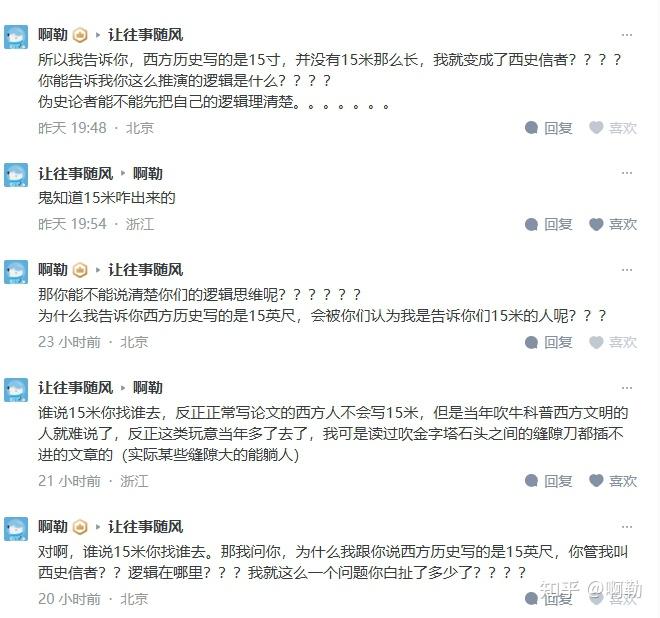
然而当一些人告诉他们,西方历史其实写的是15英尺。这些人立刻就被打成信使论者。。。。。
我一直在问那些伪史论者,这其中的逻辑是什么样的。但没有一个正面回答我的。
================================================
其实逻辑不通仅仅只是小问题,我总结果伪史论者几大问题,首要的就是思而不学。
就是坐在那里瞎想,但最重要的就是脑袋空空,没有他们所谓的“常识”
举例来说:

有人能看出来问题在哪么???问题就在于。《几何原本》里面的内容,那些定理,原本就并非欧几里得原创,而他在几何与那本中最主要的工作,就是整理了几百年间各国数学家得出的结论。而欧几里得以及几何原本的伟大,在于:
1 欧几里得把前人分散的几何知识(如泰勒斯的定理、毕达哥拉斯定理、希波克拉底的面积法、欧多克索斯的比例理论)整合为一个完整、一致、连贯的体系。
a不再是零散定理的集合,而是有明确逻辑起点和系统结构的数学体系。
b从最基础的5条公设和5条公理出发,演绎出465个命题。
c知识结构像“金字塔”,由简单向复杂推导,逻辑闭合。
这就是现代数学教育中强调“从定义出发、演绎出结果”的根本源头。
2 欧几里得是第一位将整个几何学用形式逻辑方式构建起来的人
他明确区分定义、公设、共通概念
然后,他用这些出发点,逐步演绎出全部几何结论,这种方法后来称为欧几里得式演绎法
3 欧几里得将这些内容以简洁、抽象、几何语言写成清晰可教的教材,使得被阿拉伯学者、拉丁世界、欧洲启蒙时代广泛学习;成为2000多年世界上最广泛使用的数学教科书
这就是为什么阿拉伯学者将欧几里得的几何原本视为数学思想的经典范式、逻辑推演的完美范本、伊斯兰哲学(如亚里士多德理性主义)教育的基础读物
因为几何原本的贡献,不仅仅只是解决了像是勾股定理之类的问题,他更多的是让后人更清晰的使用、学习、解读数学。
=========================================================
顺带一提,欧几里得所整理的数学家包括但不限于:
泰勒斯:最早提出几何推理思想者,欧几里得第一卷中关于三角形的基本定理(如角对边、等边三角形性质等),与泰勒斯的工作密切相关。
毕达哥拉斯学派:毕达哥拉斯定理(勾股定理)及其逆定理,出现在卷 I 命题 47,即著名的“欧几里得定理”(其实是毕达哥拉斯学派的成果)。比例理论、数的性质(如奇偶性、完全数)也见于卷 7–9。
希波克拉底:被认为是第一个系统写成《几何学原理》的人,他的工作包括:弓形面积(即不是完整圆但可求面积的区域)问题。开始了“公理化”思想的尝试
欧多克索斯:他建立了比例理论,这是欧几里得第 5 卷的基础。 特别是用比例方法解决无理数与有理数无法通用的问题。 发明了穷竭法(极限思想的雏形),为体积计算与圆面积推理铺路。他还发展了“球体、锥体、柱体”的体积理论,反映在卷 12 中。
泰阿泰托斯:研究了无理数的分类,系统地探讨了哪些根号值是无理的。他的成果构成了第10卷的主要内容,这卷是《几何原本》中技术最复杂的部分。
阿基塔斯、安提丰、德谟克利特等:探索过几何体体积、倍立方问题等。他们的研究为立体几何与立方体化问题的表述提供了素材。
======================================================
伪史论者最关键的问题,就在于他们只听说过《几何原本》,没有听说过后面这些数学家们,但不妨碍他们大胆的猜想,并将其公之于众。
如果说一个普通人,不知道也就不知道了,谁能没有一些不知道的事情。。。。。。但不知而不自知,这就是他们最大的问题。