唔……合理怀疑,这个女子参加过某个豆瓣小组,也就是“鹅组”“象组”类的小组。
我们可以看看这个问题:
这个问题,在微博的评论区怎么样呢?
我们可以发现,女性,特别是微博女性是大力支持踹男性裆部的行为。考虑到微博的信息源主要来自豆瓣,那么将微博替换成豆瓣,非常合理。
那么我们回过头来看看这件事,能发现什么呢?
在这件事里,受害者全程都保持一种比较友好的态度,反而是犯罪嫌疑人全程咄咄逼人,最后直接上脚。那么这个逻辑是什么呢?一句话概括,就是“对弱势男性进行攻击”,也符合豆瓣小组的逻辑。
那么如果能查查这个女子的社交媒体记录,说不定就能有新的发现。
那么这类的豆瓣小组,为什么要策划这些事呢?答案也很简单——在加速两极分化的社会共识中,从有利于自己的共识里吸收同伴,组成回声室,而这个回声室反过来继续加速两极分化。
那么关于这一点,我们可以看看Journal of the Royal Society Interface在2020年11月的这篇文章,文章说的是相变对社会分裂的影响。
首先要明白一点,社会凝聚力和社会碎片化是大规模社会组织和运作的核心机制。社会碎片化的机制是什么呢?主要有两种形式:一种认为碎片化是社会网络在其社会联系演变过程中出现的整体组织形式;另一种认为碎片化是相似的社会行为者基于其偏好而形成的集群。
我们假设一个社会由N个个体组成,每个个体用i来标记。每个个体都嵌入到一个社会网络中,并与ki个同伴j存在社会关系。由于我们关注的是互联互通程度对社会分裂的影响,因此我们保留了每个人的平均链接数作为模型的时间无关参数。i和j之间的关系可以是正的,如果他们是朋友,则Jij= 1;如果他们是敌人,则Jij= −1。如果两个人之间存在负向联系,则表明存在一定程度的社会压力。每个人都被赋予一个观点si。
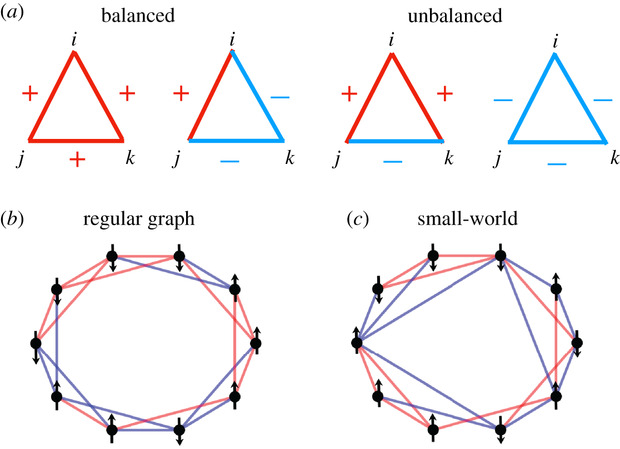
唔姆,如图所示,以上是最简单情况下的模型社会示意图。a图表示平衡和非平衡三角形。用加号表示的红线表示个体i、j和k之间的友好合作关系。(b) 图表示规则的网络拓扑结构,即每个节点都有相同数量的邻居;这里k= 4。在 (c) 中,节点与小世界网络中的其他节点相连,该网络可以通过 (b) 中的任意一条链路的一侧随机重连获得。
除此之外,还可以用哈密顿函数定义最小化的社会压力:
H=-\sum_{(i, j)} J_{i j} s_i s_j-g \sum_{(i, j, k)} J_{i j} J_{j k} J_{k i}
其中si∈ { − 1, 1} 表示个体i的观点,Jij∈ {1, − 1} 分别表示两个关联主体i和j之间的友好程度和敌意程度(如果它们之间没有关联,则Jij= 0)。

唔姆,如图所示,以上是社会压力H如何在四个个体的观点和联系变化过程中逐渐降低的示意图。节点的观点用 ↑ 和 ↓ 表示,正向联系用红色表示,负向联系用蓝色表示。
因此,通过 Metropolis 算法实现观点和链接的同步演化,这是物理学中最小化系统哈密顿量的标准程序。
社会从一个时间步t到下一个时间步的更新方式如下:
1.计算系统当前状态的H,假设它的值为H 0。
2.随机选取一个节点i并翻转其观点s i。再次计算H 值,此时为H 1 。如果H值因翻转而下降,即H 1 ≤ H0,则接受翻转。如果H值上升,则以概率p = e−ΔH / T接受翻转,其中ΔH= H1−H0是翻转前后的压力差。T表示“社会温度”,是一个模型参数。随机选取下一个节点,并继续操作,直至完成N× n次观点更新。
3.计算此时系统的H ,假设它现在是。现在我们随机选择一个链接J ij,并将其翻转。再次计算H ,并假设它是,我们接受翻转,如果并有概率接受它, 在哪里, 如果。为简单起见,我们假设T与步骤 2 中的相同。
4.继续下一个时间步骤。
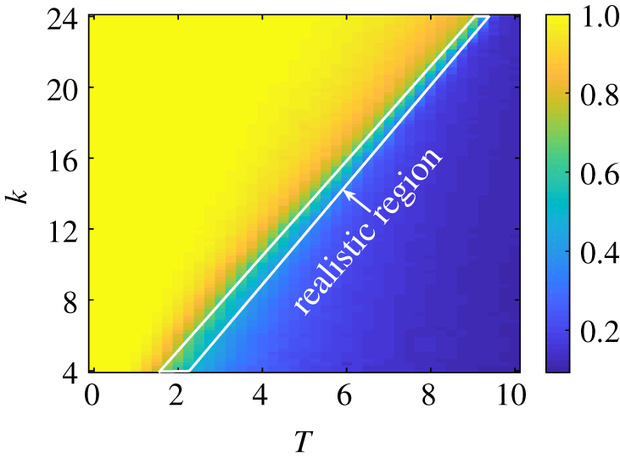
唔姆,如图所示,以上是具有社会平衡的随机协同进化模型的相图。平衡水平f表示为平均网络度k和社会温度T的函数。
结论很明显,图中有一条清晰的分界线,在这个区域中,社会从f∼ 0.1(蓝色)的连贯状态转变为f∼ 1(黄色)的碎片化状态。在黄色区域中,新兴网络是高度平衡的,存在意见集群。在深蓝色区域中,这些极化的集群消失,意见在代理之间随机分布,其中平衡三角形的数量与不平衡三角形的数量一样多。需要注意的是,f ∼ 0 的值是不现实的。现实社会是平衡的,其经验值在f∼ 0.7左右的范围内。我们用白色方框表示现实区域。假设某个社会位于现实区域的某个位置,比如在某个固定的T下,只需社会连通性k略有增加,社会就会进入碎片化阶段。
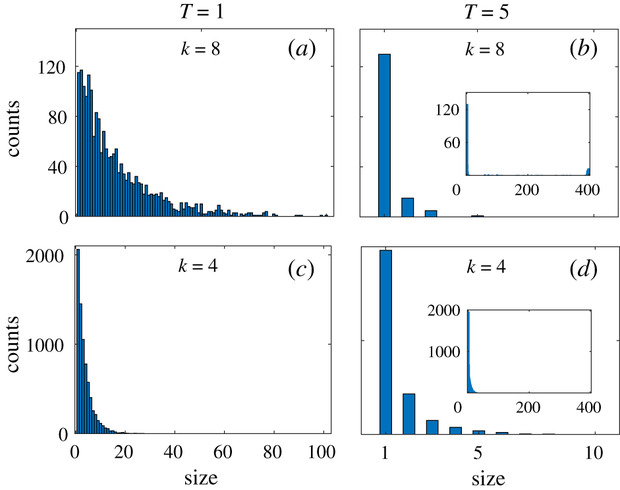
唔姆,如图所示,以上是不同T和k值下的回声室大小分布。左栏显示社会温度较低(T= 1)的情况,右栏显示温度较高(T= 5)。上图显示平均连通性较高(k= 8),下图对应于k= 4 的邻居。左栏对应于碎片化阶段,右栏对应于凝聚阶段。
结论很明显,在碎片化阶段的深处,我们观察到回声室大小分布广泛,k = 8 时约为 100,k= 4时约为 20。右栏中,峰值分布较为明显,最大簇大小约为 2-3,这意味着没有形成大型的独特观点簇。这对应于一个不同观点共存的社会。当然,k=8和4的对比条件下,当k更大时,明显社会更加碎片化。
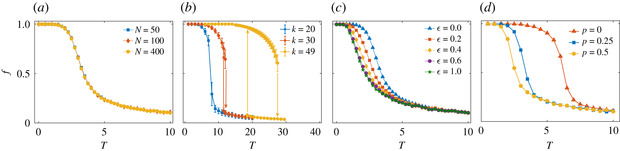
唔姆,如图所示,以上是结果的稳健性。(a)图表示规模依赖性。不同社会规模(N= 50、100、400)的常规网络相图截面(k = 8)。相图中看不到尺寸依赖性。对于固定值k = 8,我们在图a中展示了常规网络上不同系统规模N= 50、100、400 的相图剖面。在考虑的N范围内,未观察到任何规模依赖性。缺乏规模依赖性可能表明,对于此类网络拓扑结构,在N→ ∞的极限下,结果可能仍然成立。[1]
那么我们就可以发现,促进社会碎片化的两个主要因素,一个是增加成员连通性,一个是降低社会温度,也就是改变成员观点的概率。
那么,这件事的作用是什么呢?我们如果将这件事设想成一个公共回声室,那么这件事的发生,在涉事女子最后没有受到惩罚的情况下,相当于增加了豆瓣小组观点的连通性,即大量扩散了“踢裆无罪”的观点。
当然,在回声室中,回声室成员的社会温度极低,而且在接受了其他地方的反对声音后,反而会进一步降低社会温度。
我们可以看看PNAS在2018年8月的这篇文章,文章的内容暴露于社交媒体上的反对意见会加剧倾向两极分化。
研究人员选取了1,652个用户。在实验里,通过创建一个进步推特机器人和保守推特机器人,给双方推送相反倾向的推特。
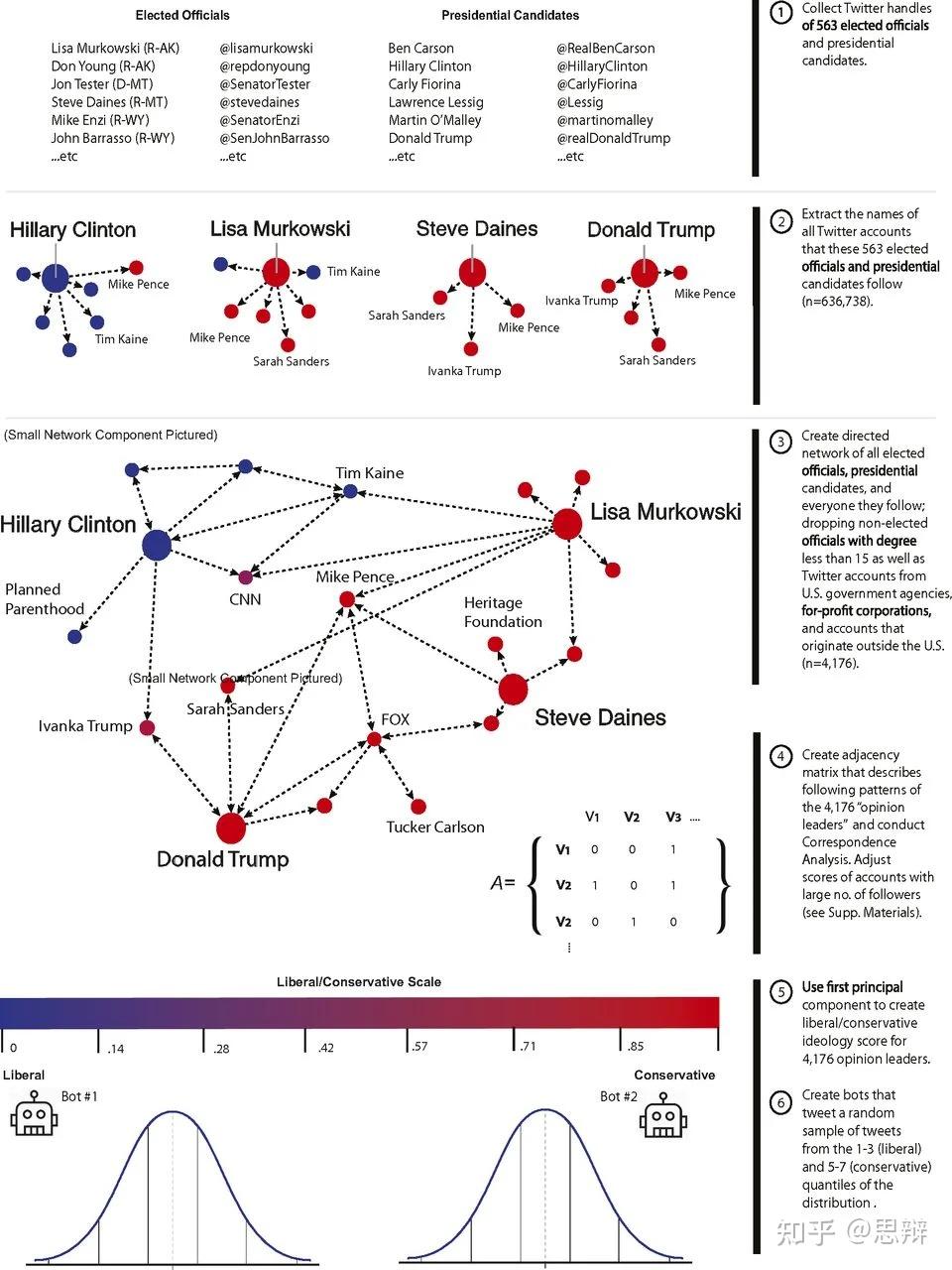
结论如下:
双方在接受推送后,会继续深化倾向。而且共和党会呈现出激进的观点。
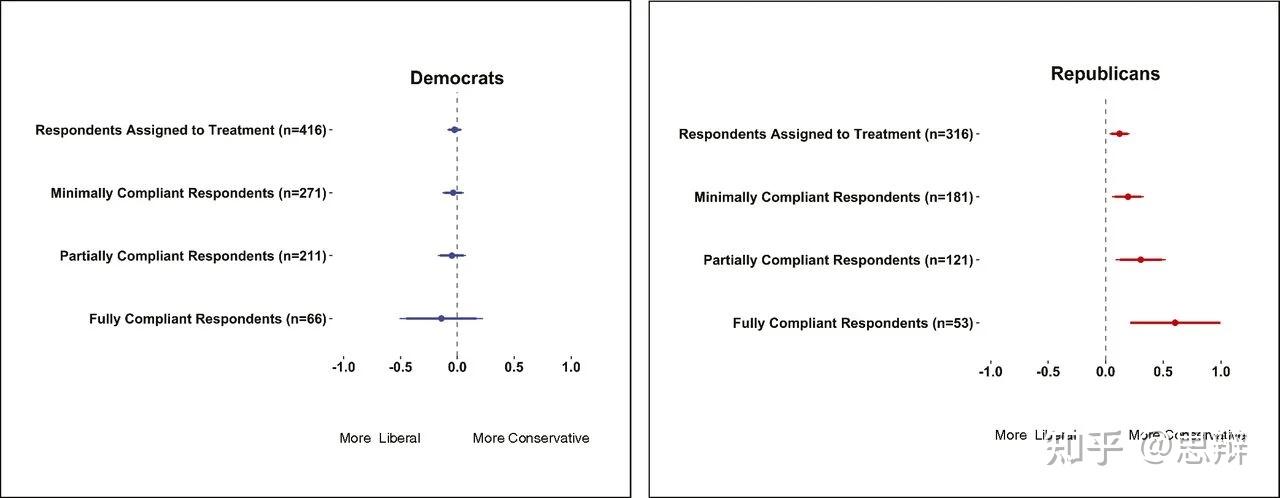
[2]
结论很明显,在接触反对观点后,回声室的成员反而会更固执,更难改变自己的意见。那么二者因素叠加起来,这件事的后果,就是进一步加剧社会共识两极分化。
参考
- ^Minh Pham Tuan, Kondor Imre, Hanel Rudolf and Thurner Stefan 2020The effect of social balance on social fragmentationJ. R. Soc. Interface.1720200752
- ^C.A. Bail,L.P. Argyle,T.W. Brown,J.P. Bumpus,H. Chen,M.B.F. Hunzaker,J. Lee,M. Mann,F. Merhout,& A. Volfovsky, Exposure to opposing views on social media can increase political polarization, Proc. Natl. Acad. Sci. U.S.A. 115 (37) 9216-9221, https://doi.org/10.1073/pnas.1804840115 (2018).